Ford's Touching Circles
by Rita Snyder, Matt Sorrells, and B.J. Jackson
The challenge is to construct three circles tangent
to each other and to a given line.
At first this seems impossible until we look at some
equations. First we find two points on the given line a/b and
c/d such that a+d = b+c. To help illustrate this we will use the
points where a=1, b=2, c=2, and d=3.

Now we want to find a point such that (a+c)/(b+d)so
for our example our third point will be 3/5. In order to locate
this point we must cut the segment between 1/2 and 2/3 into 5
equal parts.
To do this we will first construct an arbitrary line
through point A.
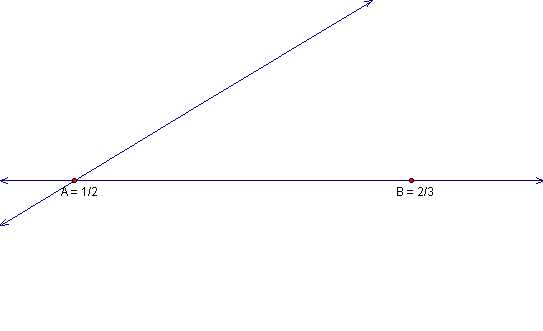
We then construct a circle with center A
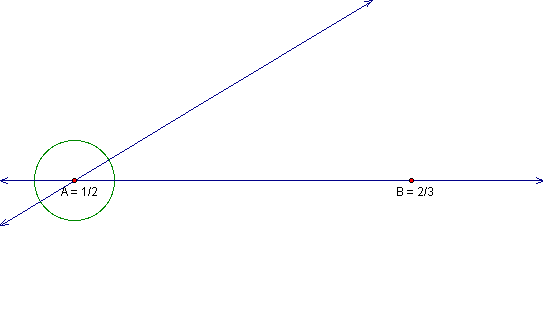
Locate where the circle intersects the arbitrary line
and construct another circle with the center as the point of intersection
and the radius equal to that of our first circle.
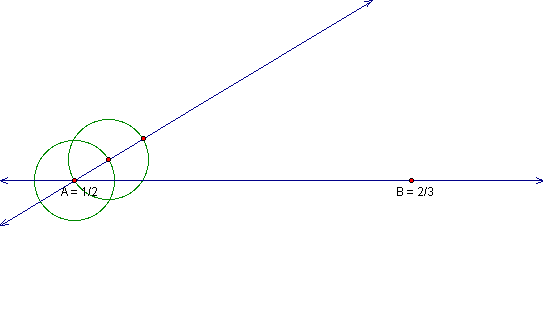
Continue this construction process until you have
identified five points of intersection on our arbitrary line.
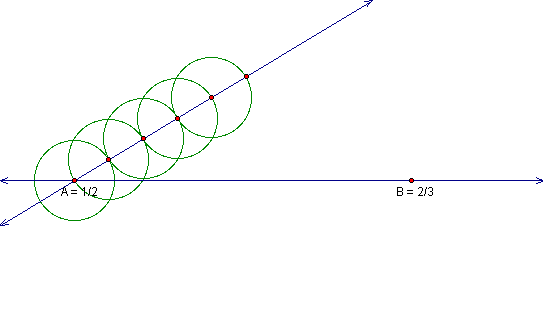
Now construct a line through our fifth point of intersection
and our point B.
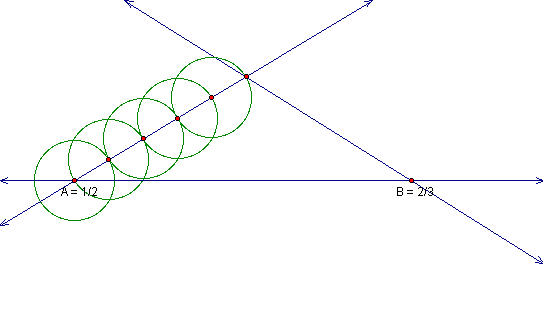
Construct lines through our other four points parallel
to our new line and identify the points where our parallel lines
intersect our given line
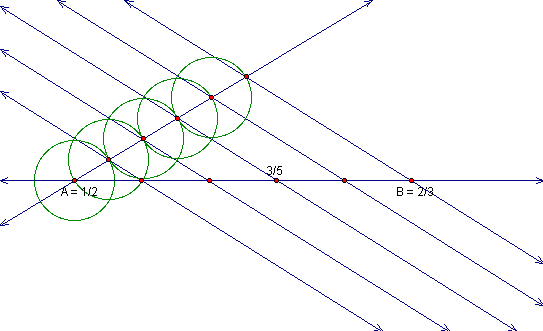
Now we can identify our point 3/5

.
Next we want to construct circles through points A and B tangent
to the line such that if we say the points A and B equaled p/q,
the diameter of the circle would equal 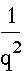 .
In order to get the correct ratio we need to solve
.
In order to get the correct ratio we need to solve 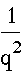 =
x/30 (the common denominator of 1/2, 3/5, and 2/3). So for our
example we need to solve 1/4 = x/30 thus 4x = 30, so x=15/2 or
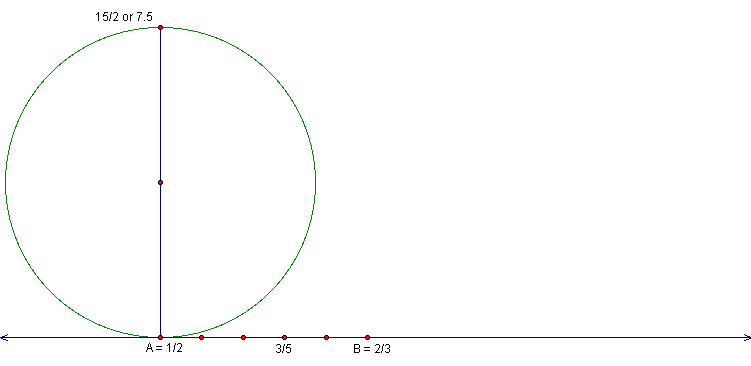
7.5 to construct the circle through point A.
=
x/30 (the common denominator of 1/2, 3/5, and 2/3). So for our
example we need to solve 1/4 = x/30 thus 4x = 30, so x=15/2 or
7.5 to construct the circle through point A.
Once we have determined the value of x, we then construct
our circle such that it is tangent to our given line. In order
to ensure tangency, we construct a line perpendicular to our given
line through point A.
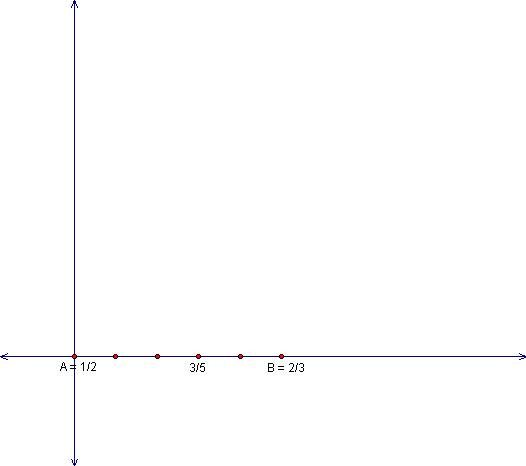
Then construct a circle with center A and radius equal
to 1/5 of our given segment and identify the point where the circle
intersects our perpendicular line. Now construct another circle
with the center as the point of intersection and radius same a
previous circle.
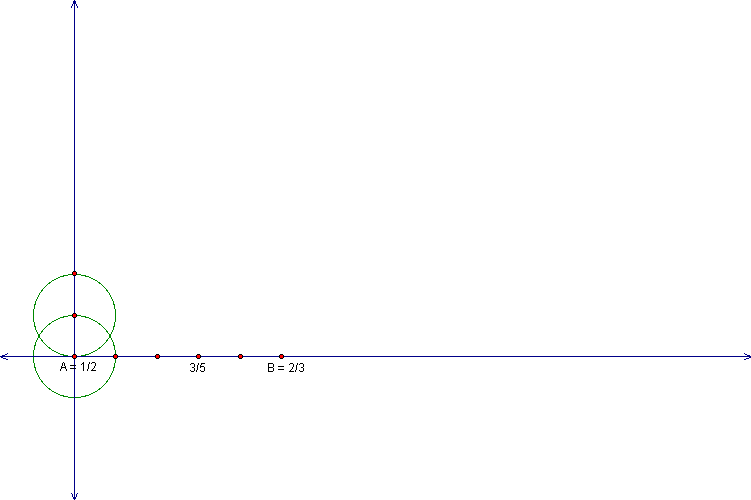
Continue this process until there are 8 points of
intersection.
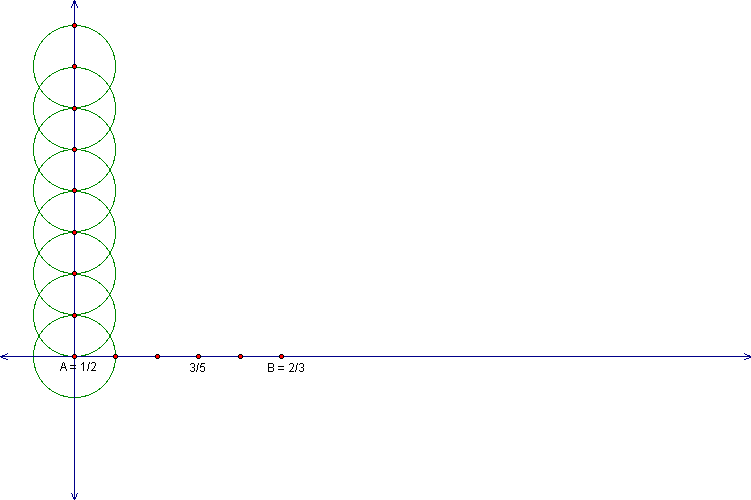
Then find the midpoint between the 7th and 8th point
of intersection. The distance from this midpoint and point A is
equal to 15/2 or 7.5, thus it is the diameter of your circle tangent
to the given line.
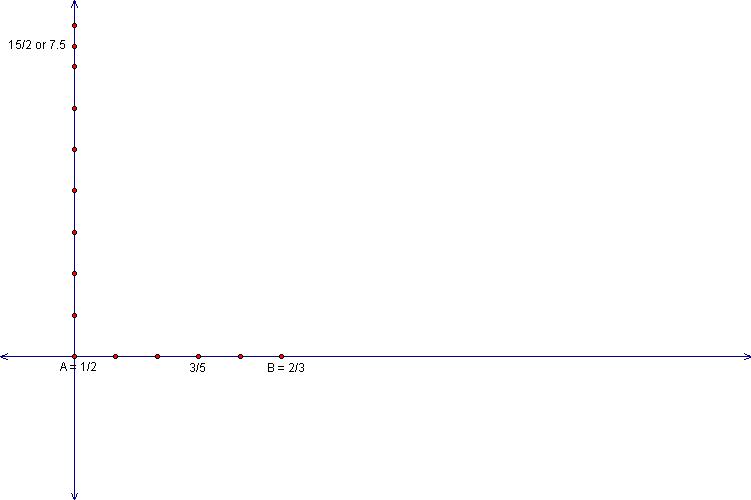
If you find the midpoint of this diameter you can
construct your first Ford Circle.
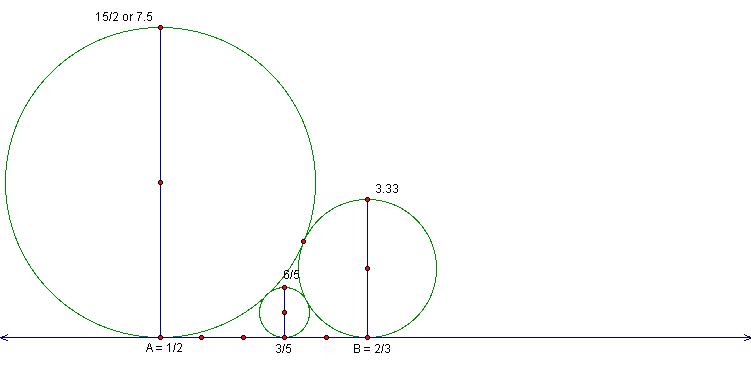
Use this same process to construct the circle through
point B that is also tangent to the given line. The same process
can be used to construct the circle through our point labeled
3/5.
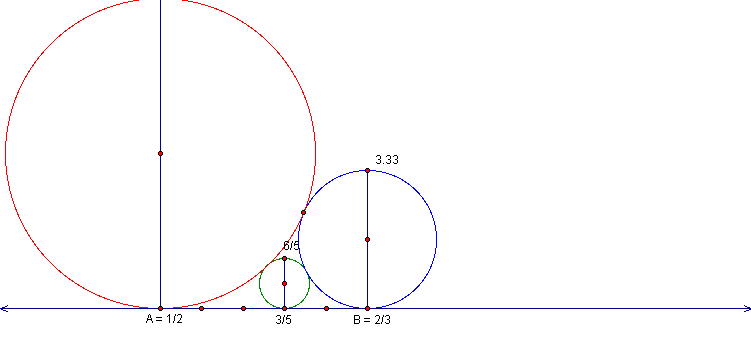
To verify that our constructions are correct we'll
use the construction method for constructing a circle tangent
to a given circle and a given line.
We will use our three Ford's circles and the given
line to reconstruct tangent circles to our circles and given line
see if they appear in the same location. We'll recolor the circles
to make them more identifiable.
First lets start with our red circlewe want to construct
a circle tangent to the red circle given our line and we want
the new circle to intersect the point 2/3 on our given line.
The first thing we do is construct a line perpendicular
to our given line through point 2/3, then construct a circle with
the center at point 2/3 and the radius equal to that of our red
circle.
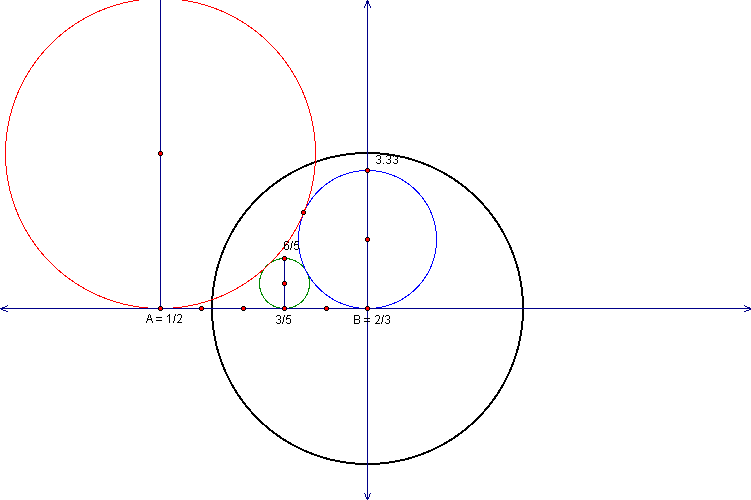
Now label the points where the new circle intersects
the perpendicular line point J and K. Then construct a segment
from the center of our red circle to point K and construct a perpendicular
bisector to this segment.
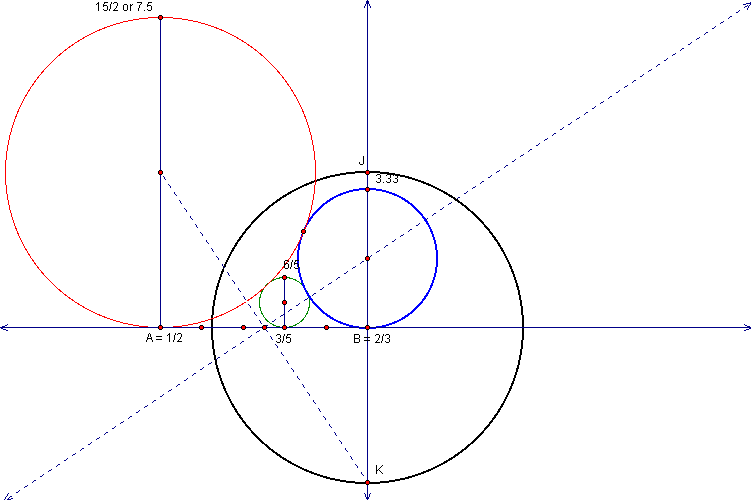
The point where our perpendicular bisector crosses
our first perpendicular line is the center of our new circle,
if you notice it is exactly where the center of the blue circle
is located.
We'll now use the same contruction method with our
blue circle being the given circle and our given line, and using
the point 3/5 for a new tangent circle.
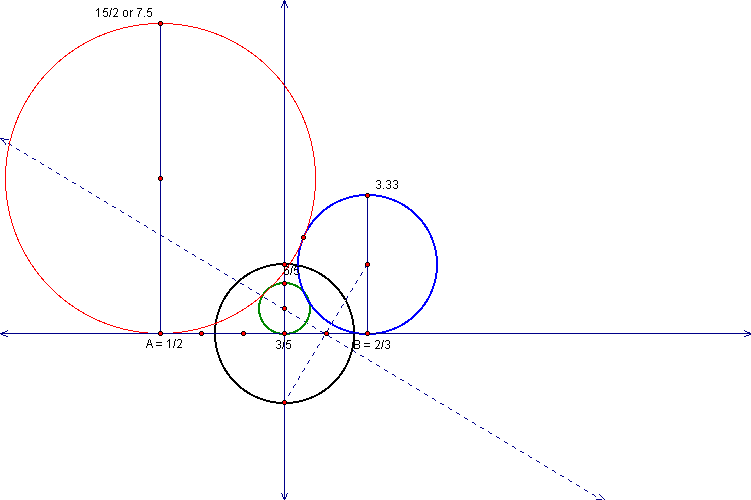
Again you see that where our perpendicular bisector
crosses our first perpendicular line is exactly where the center
of the green circle is located.
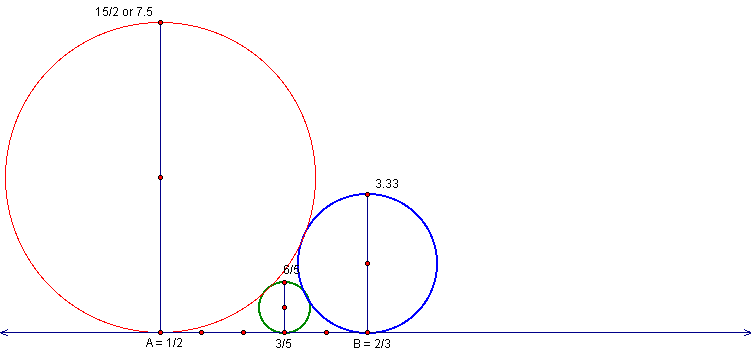
Thus our first method of constructing our Ford's Touching
Circles is accurate.
















