Areas of Rhombuses and Kites

By

Troy Morris

The rhombus and kite are two quadrilaterals that are not quite as common as other quadrilaterals, like the rectangle and square. However, they are still important in the studies of geometry, including that of area. We will discuss the area formulas later and I will present some problems I would like you to attempt. I would first like to define each of these polygons and give illustrations of what each figure looks like.

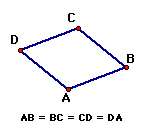
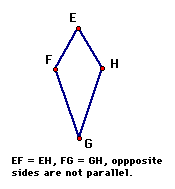
RHOMBUS- a quadrilateral in which all four sides are congruent.

KITE- a quadrilater in which each pair of consecutive sides are congruent, but opposite sides are not congruent.

FORMULAS- The reason these two polygons were grouped together is because they actually have the same formula for their areas. In order to find the formula for their areas, diagonals must be constructed to each pair of opposite vertices. The area then equals half the product of the two diagonals.

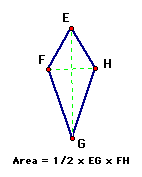
The same formula is used to find the area of a rhombus as well.

PROBLEMS- Solve the following problems involving rhombuses and kites.

1) In a kite, diagonal 1 = 8 cm, diagonal 2 = 6 cm, find the area.

2) In a rhombus, diagonal 1 = 14 in., diagonal 2 = 18 in., find the area.

3) In a rhombus, the area = 198 sq. cm., diagonal 1 = 7 cm, find diagonal 2.

RETURN