

Maximize the volume of a lidless box formed from 5x8 sheet with a square (with a length of x) removed from each corner.
Using the figure above, the dimensions of the box are
The formula for the volume of this box would be
Use a spreadsheet to display possible values of x, (8-2x), (5-2x), and V.
| x | 8-2x | 5-2x | V=x(8-2x)(5-2x) |
| 0 | 8 | 5 | 0 |
| 0.1 | 7.8 | 4.8 | 3.744 |
| 0.2 | 7.6 | 4.6 | 6.992 |
| 0.3 | 7.4 | 4.4 | 9.768 |
| 0.4 | 7.2 | 4.2 | 12.096 |
| 0.5 | 7 | 4 | 14 |
| 0.6 | 6.8 | 3.8 | 15.504 |
| 0.7 | 6.6 | 3.6 | 16.632 |
| 0.8 | 6.4 | 3.4 | 17.408 |
| 0.9 | 6.2 | 3.2 | 17.856 |
| 1 | 6 | 3 | 18 |
| 1.1 | 5.8 | 2.8 | 17.864 |
| 1.2 | 5.6 | 2.6 | 17.472 |
| 1.3 | 5.4 | 2.4 | 16.848 |
| 1.4 | 5.2 | 2.2 | 16.016 |
| 1.5 | 5 | 2 | 15 |
| 1.6 | 4.8 | 1.8 | 13.824 |
| 1.7 | 4.6 | 1.6 | 12.512 |
| 1.8 | 4.4 | 1.4 | 11.088 |
| 1.9 | 4.2 | 1.2 | 9.57599999999999 |
| 2 | 4 | 0.999999999999999 | 7.99999999999999 |
| 2.1 | 3.8 | 0.799999999999999 | 6.38399999999999 |
| 2.2 | 3.6 | 0.599999999999999 | 4.75199999999999 |
| 2.3 | 3.4 | 0.399999999999999 | 3.12799999999999 |
| 2.4 | 3.2 | 0.199999999999998 | 1.53599999999999 |
| 2.5 | 3 | 0 | 0 |
We only need to use values of x<2.5 since the width is 5 and using a larger value of x would give us a negative number and the sheet would disappear.
Looking at the Volume column shows that the volume appears to reach a maximum volume of 18 when x=1.
This is supported using the first derivative of V.
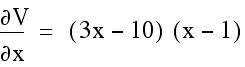
The first derivative of V gives the critical points of 1 and 10/3. The value of 1 is the only value between 0 and 2.5.
Using the second derivative of V,
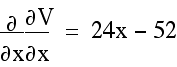
the value is positive when x=1 and that means V is a maximum at that value.
This can also be verified by the graph of the equation
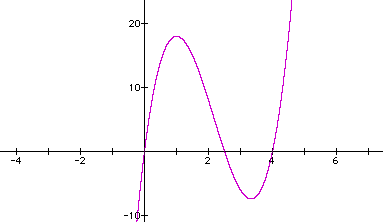
At x=1, the graph shows a relative maximum point.
Return to Class Page