

Observe the graph of the quadratic equation
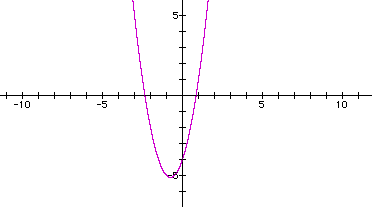
i) Overlay a new graph onto the original by replacing each x by (x-4).
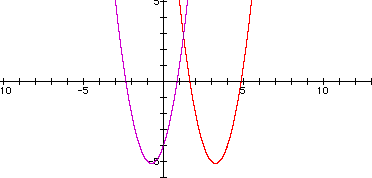
The new graph (in red) appears to have displaced the original graph 4 units to the right.
Algebraic manipulation of the equation yields a simplified form of
![]()
![]()
![]()
ii) Change the original equation to move the graph into the second quadrant.
Begin with
Notice from part i that by changing the coefficient of x and the constant, the graph shifted toward the fourth quadrant.
Try
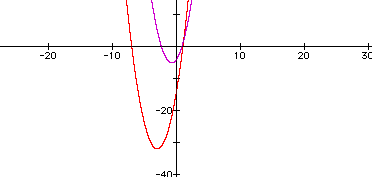
The graph was shifted into the third quadrant.
Now try
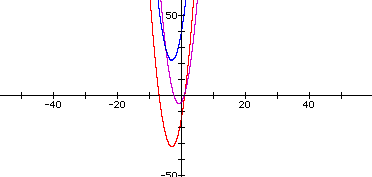
By increasing the coefficient of x and the constant term, the graph shifted to the second quadrant.
Also, consider
to see if the graph can be moved to the second quadrant. Since (x-4) shifts the graph to the right, try replacing x by (x+4).
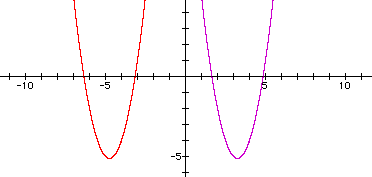
This shifted the graph to the left into the third quadrant.
Try
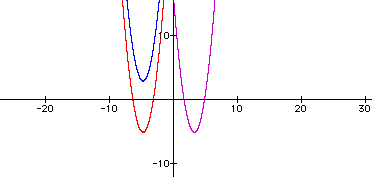
By changing the constant to +4, the graph was shifted up into the second quadrant.
This seems to show that using the factored form of the quadratic equation makes it easier to shift the graph from one quadrant to another.
iii) Change the original equation to produce a graph concave down that shares the same vertex with the original graph.
Consider the equation
Change to
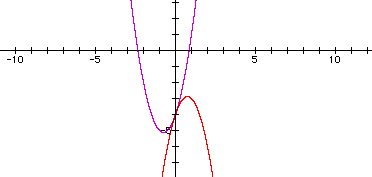
The graph needs to be moved down and to the left.
Try
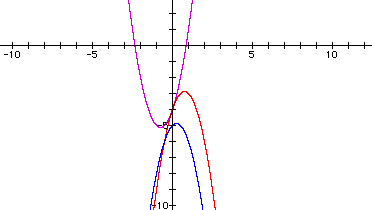
Now try
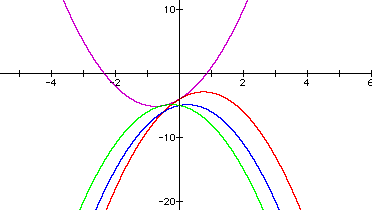
The graph appears to be moving toward sharing the same vertex. Using the assumption from part ii about the factored form of the equation, rewrite the equation in standard parabolic form.
This gives a vertex at (-3/4, -5 1/8).
Change to
Use algebra to rewrite as
The new graph is
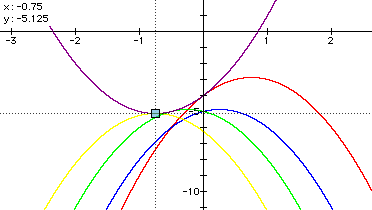
This graph is concave down and shares the same vertex as the original.
Also consider
Change coefficients to
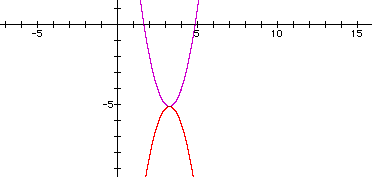
By using the same coefficients the graph yields a concave down curve that shares the same vertex.
Return to Class Page