The CIRCUMCENTER (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle.

Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle.

Construct the circumcenter C of an acute triangle.

First, find the midpoints of each segment.

Then, construct the perpendicular bisectors of each side of the triangle.

The point of intersection is the circumcenter.

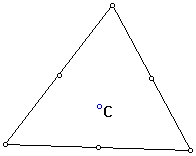
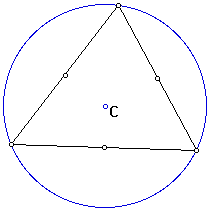
The location of the circumcenter (C) in an acute triangle is in the interior of the triangle.

It is the center of the CIRCUMCIRCLE of the triangle, that is, the circumscribed circle.

Construct the circumcenter (C) of a right triangle.

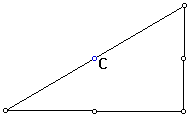
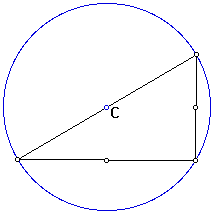
The location of the circumcenter of a right triangle is at the midpoint of the hypotenuse of that triangle.

The hypotenuse of the the right triangle is the diameter of the circumcircle.

Construct the circumcenter (C) of an obtuse triangle.

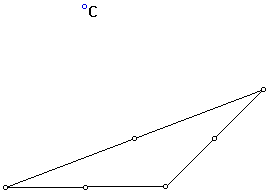
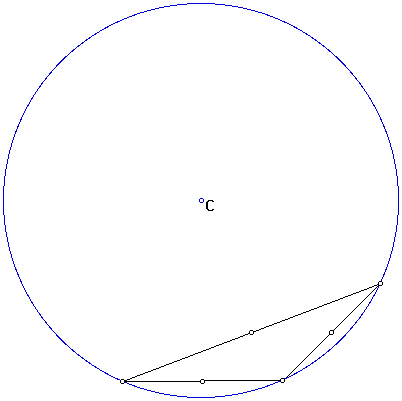
The location of the circumcenter of an obtuse triangle is in the exterior of the triangle.

The circumcircle has its center at the circumcenter of the triangle.

Return to Class Page