
By Nami Youn

By Nami Youn
Write-up #8
Altitudes and Orthocenters
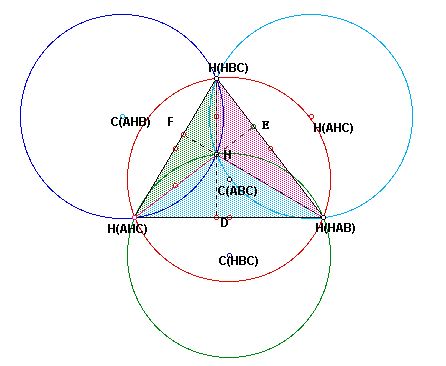
Given a triangle ABC, I will construct the Orthocenter
H of triangle ABC and then the Orthocenters of each triangle HBC, HAB,
and HAC. The four circles are the circumcircles of triangelks ABC, HBC,
HAB, and HAC.
Click here for a GSP sketch.
Prove that
(1)
HD/AD + HE/BE + HF/CF = 1
(2) AH/AD
+ BH/BE + CH/CF = 2
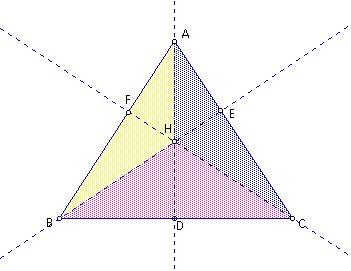
(1) HD/AD + HE/BE + HF/CF = 1
Let the area of ABC = S, are of HAB = S1, area of HBC = S2, and area of HCA = S3. Then
S = 1/2 AB*CF = 1/2 BC*AD = 1/2 CA*BE
S1 = 1/2 AB*HF
S2 = 1/2 BC*HD
S3= 1/2 CA*HE
Since S = S1 + S2 + S3, we can obtain
1 = (S1 + S2 + S3)/S = S1/S + S2/S + S3/S = HF/CF + HD/AD + HE/BE
Therefore, HD/AD + HE/BE
+ HF/CF = 1
(2) AH/AD + BH/BE + CH/CF = 2
Since HD = AD - AH, HE = BE - BH, and HF = CF - CH, and by the fact (1)
1 =
HD/AD + HE/BE + HF/CF
= (AD - AH)/AD + (BE - BH)/BE + (CF - CH)/CF
= 3 - (AH/AD + BH/BE + CH/CF)
Therefore, AH/AD + BH/BE + CH/CF = 2
In an obtuse triangle, the orthocenter is outside of the
given triangle. In the below figure, the point H is the orthocenter
and therefore the relationship (1) and (2) cannot be true any more.
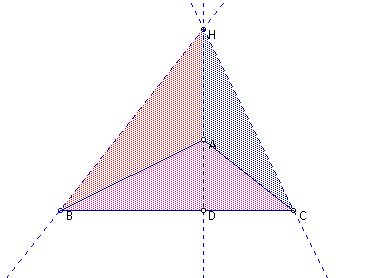
However, the point A is the orthocenter of triangle HBC. So we can adjust the previous relationships as below.
(1) AD/HD + AE/BE + AF/CF
= 1
(2) AH/HD + BA/BE + CA/CF
= 2