
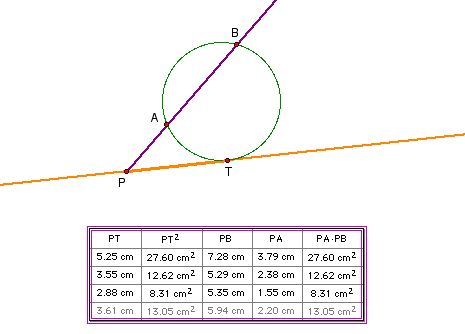
Property 1
From a point outside a circle,
construct the tangent and secant line.Let the intersection point of the
tangent and the circle be T. Let the intersection points of the secant
and the circle be A and B. Then, PT PT =PAPB
If the points A and B lie on
the half line with point P as an endpoint and point T does not lie on this
half line, PT PT =PAPB, then the line PT is a tangent line of this circle
passing through A, B, and T.
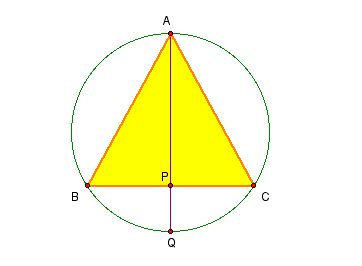
Isosceles triangle
ABAB =ACAC=APAQ
The common tangent line of two
circles
PAPB = PCPD
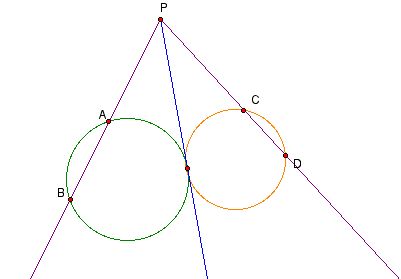
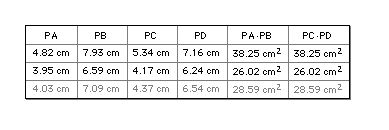
Let the intersection point of extension lines of two chords AB and CD
in a circle be P. If PAPB = PCPD, then the four points A, B, C, and D lie
on a circle.