


First let's prove that all points on the perpendicular bisector are equidistant from A and B.
We want to show
that the perpendicular bisector of AB, passing through midpoint
M of AB, is the set of all points that have equal distances to
A and B.
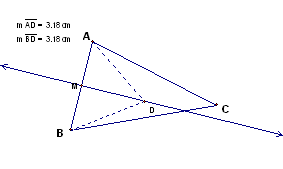
Let D be any point on the
perpendicular bisector, then we want to show AD is congruent
to BD. Since M is the midpoint of AB, then
AM is congruent to BM. And DM is congruent
to DM.
< BMD is congruent to < AMD since line DM
is the perpendicular bisector.
By SAS, we have the triangles BMD is congruent to
AMD.
Therefore, AD is congruent to BD and all the
points on the perpendicular bisector are equidistant from A and
B.
Now we want to show that all points that are equidistant from A and B lie on the perpendicular bisector.
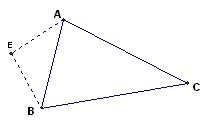
Let the point
E be any point that is equidistant from the point A
and the point B.
Then EA is congruent to EB and triangle AEB
is an isosceles triangle.
The line through < BEA that is perpendicular to the
opposite side, AB, intersects AB at its midpoint,
M.
Therefore, point E is on the perpendicular bisector of AB and we have proved that all points that are equally distant from A and from B lie on AB's perpendicular bisector.
We still have yet to prove that all the perpendicular bisectors are concurrent though. But what we have just proved is true for the perpendicular bisectors of AC and BC (I.E. )
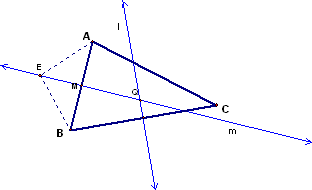
Let the line l be the perpendicular bisector of AB
and line m be the perpendicular bisector of BC.
Let the point Q be the point of intersection of line l and
line m. Then be what we have proven, QA is
congruent to QC.
******
Thus, all three perpendicular bisectors are concurrent.
Return to Laurel's Homepage
