 |
 |
 |
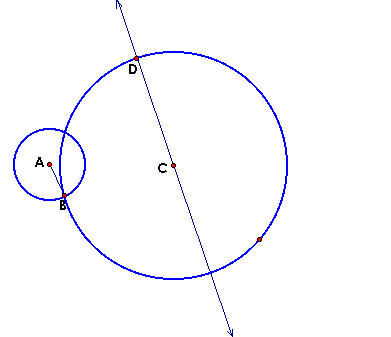
Given: The center of the desired circle will lie along a line from the center of the given circles with the specified point. |
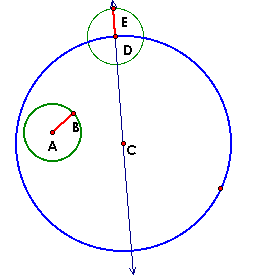
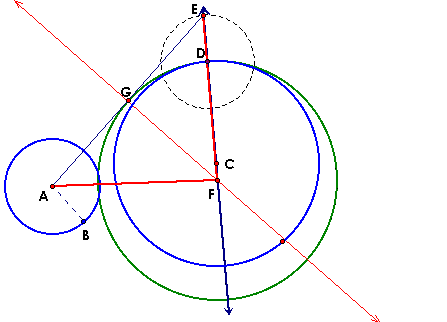
Take the radius of the smaller circle (AB) and construct another circle with the same radius measure centered at point D. |
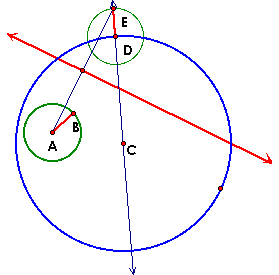
Construct a segment from point A (center of the smaller cirlce) and point E - point of intersection of the constructed circle and line through the center of the larger circle. Then construct the perpendicular bisector for this segment. |
 |
 |
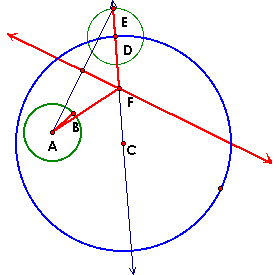
Why does this work? By construction, point G is the midpoint of segment AE. Therefore |AG| = |GE|. Additionally, GF is perpendicular to AE creating two congruent triangles (triangle AGF and triangle EGF). The |AF| = |EF|. Since by construction, |AB| = |DE|, it follows that |BF| = |DF|. By creating a circle with center F whose radius has length |BF|, we will always have a circle tangent to both circles at the points B and D. |
Find the point of Intersection with the perpendicular bisector and the line through the center. This becomes the center of the tangent circle. |
Construct a circle centered at point F, with a radius of FD. (Recall point D is the point we want the constructed circle to be tangent to) |
Question: What if E was a different point? Would the same arguement hold? |
Proof that the locus is an ellipse with foci points A and C which are the centers of the two original circles: |
|AF| = |FE| by congruency of triangles.|FD| = |FC| which is the radius of the big circle.|AB| = |DE| which is the radius of the small circle.Therefore, |AF| + |FC| = |FD| + |FE| = |FC| + |FE| = |CD| +|DE|, which is constant because it is the radius of the big circle plus the radius of the small circle.By the geometric definition of the ellipse, the locus created is an ellipse. |
 Click Here
for an animation.
Click Here
for an animation.  |
 |
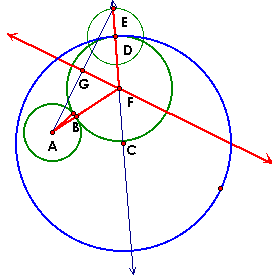
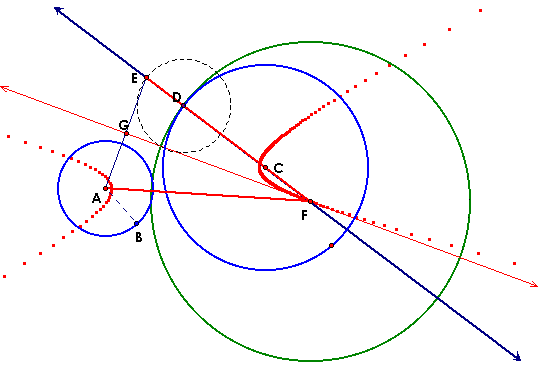
GIVEN TWO CIRCLES DISJOINT, CONSTRUCT A TANGENT CIRCLE TO BOTH |
THE CONSTRUCTION OF THE TANGENT IS DONE IN A SIMILAR MANNER AS ABOVE. |
 |
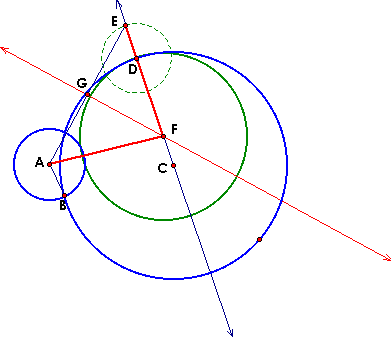
The locus seems to be a hyperbola. In let's proof that is it a hyperbola with foci points A and C.PROOF: |AF| = |EF| by construction.|DE| = |AB| by construction.|AF| - |FC| = |EF| - |FC| = |EC| = |ED| + |CD| which is the sum of the radii of the original circles which is a constant.Therefore, by the geometric definition of a hyperbola, the locus is a hyperbola. |
 |
 |
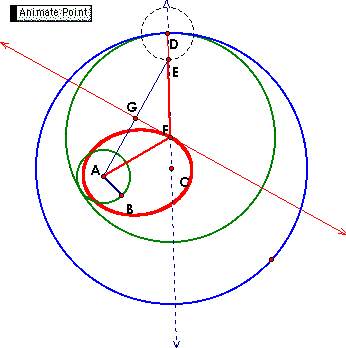
GIVEN TWO CIRCLE INTERSECTING, CONSTRUCT A TANGENT CIRCLE |
THE CONSTRUCTION OF THE TANGENT IS DONE IN A SIMILAR MANNER AS ABOVE. |
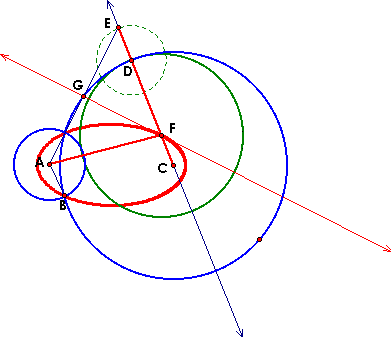 |
The locus appears to be an ellipse with foci A and C.Proof:|AF| = |FE| by construction|AB| = |DE| by construction|AF| + |FC| = |EF| + |FC| = |CE| = |CD| + |DE| = |CD| + |AB|, which is the sum of the sum of the radii of original circles.
By the geometric definition of the ellipse, the locus is an ellipse with foci A and C, the centers of the original circles. |