The above equation is known as a quadratic equation.  A quadratic equation is an equation that can be expressed in the form of:

where a is not equal to zero.

Every quadratic equation has U-shaped graph called a parabola.  

In this exploration, I want to investigate when b = 1, and c = 2 and the value of a changes.   Thus we have the equation:  .

Let's begin by choosing various values of a - positive and negative:
a=1; a=-1; a=3; a=-3; a=10; a=-10

Initially, we notice that when a is positive, the parabola opens upward; and when a is negative it opens downward.   

Additionally, from the above graph, it appears that the point (0,2) is common to all the parabolas.  Which can be easily proven by the fact that when x = 0 (no matter the value of a), the equation becomes y = 2. So the point (0,2) is common to all the parabolas.

What happens, though, as |a| gets bigger or smaller?  Let's graph more values for a, where a is getting increasingly larger:  
a = 1, a = 3, a = 5, a = 10, a =20.

It is apparent that as |a| increases, the parabola narrows.  Similarly, as |a| decreases, the parabola widens.   So as the parabola widens, will this parabola ever cross the x - axis?    And if so, where?   

Using the quadratic formula, we can find the roots for the function  .   In the equation (b=1,c=2),  the roots are

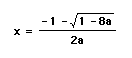and . When will the roots be real? When the discriminant (1- 8a) > 0, so when a < 1/8 is when there will be real roots and when a = 1/8, then x = -4. Let's look at this pictorially, let a = 1/8 and a = 1/16.

But what happens when a = 0?   The equation then becomes y = x + 2,  which is a linear equation, and is no longer a quadratic equation  (refer to the definition stated at the top).   Let's graph this linear with a few of the above parabolic equations:

Like the parabolas, the line also passes through the point (0,2).

Let's take a look at other sets of graphs when b=2, c=1, again varying a:

a=1; a=-1; a=3; a=-3; y=2x+3