COST OF A STAMP

 

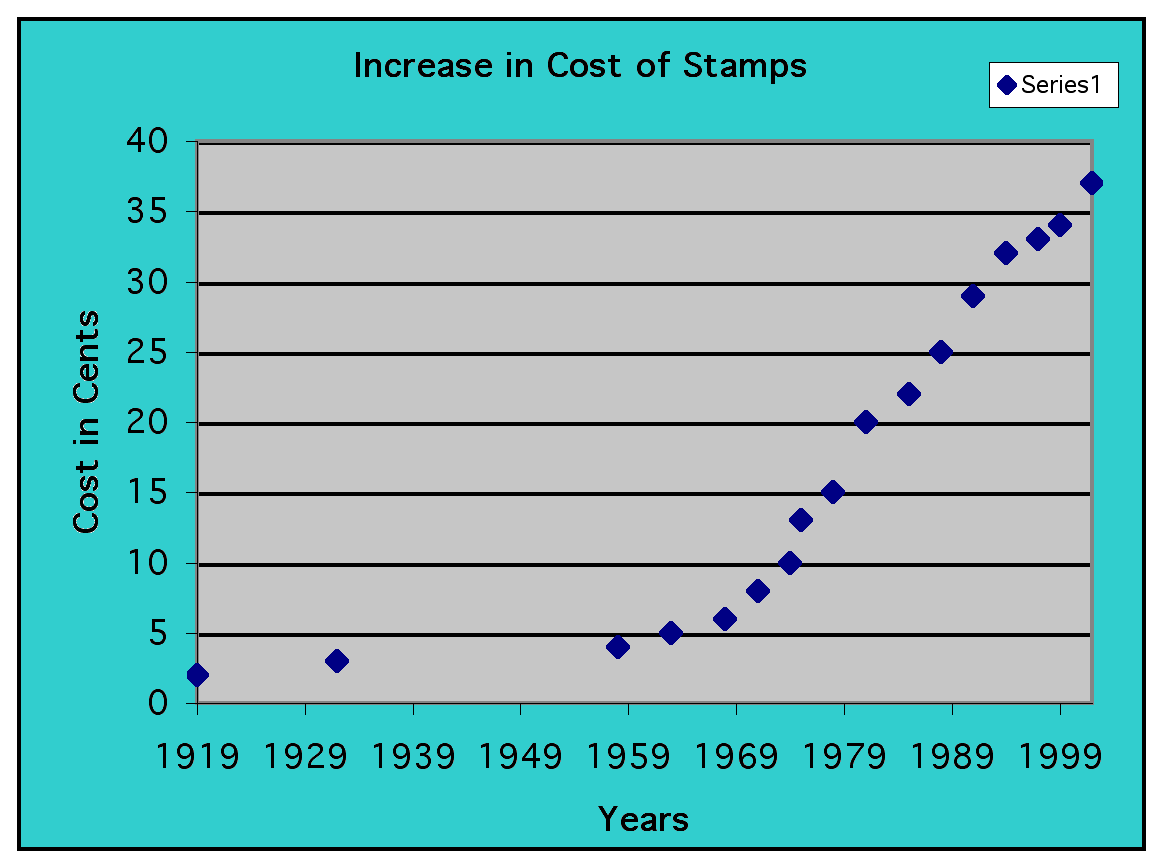
The following data set is based on the first class letter postage for the US Mail from 1933 to 1996.

 

Year

Rate(in cents)

1919

2

1932

3

1958

4

1963

5

1968

6

1971

8

1974

10

1975

13

1978

15

1981

20

1985

22

1988

25

1991

29

1994

32

1997

33

1999

34

2002

37

By plotting the points, we can look at the increase as shown on the graph.

 

Can we find a function to fit the graph of the data shown? Is it a power function, exponential, logarithmic, polynomial? It appears to be exponential, but we need to look at some other graphs.

A power function is of the form y = ax^b

We begin with the form for the power function and take the logarithm of both sides:

log y = log(ax^b)

If we let log y = Y and log a = A, then we recognize that this is the form of a linear equation

Y = A + bx

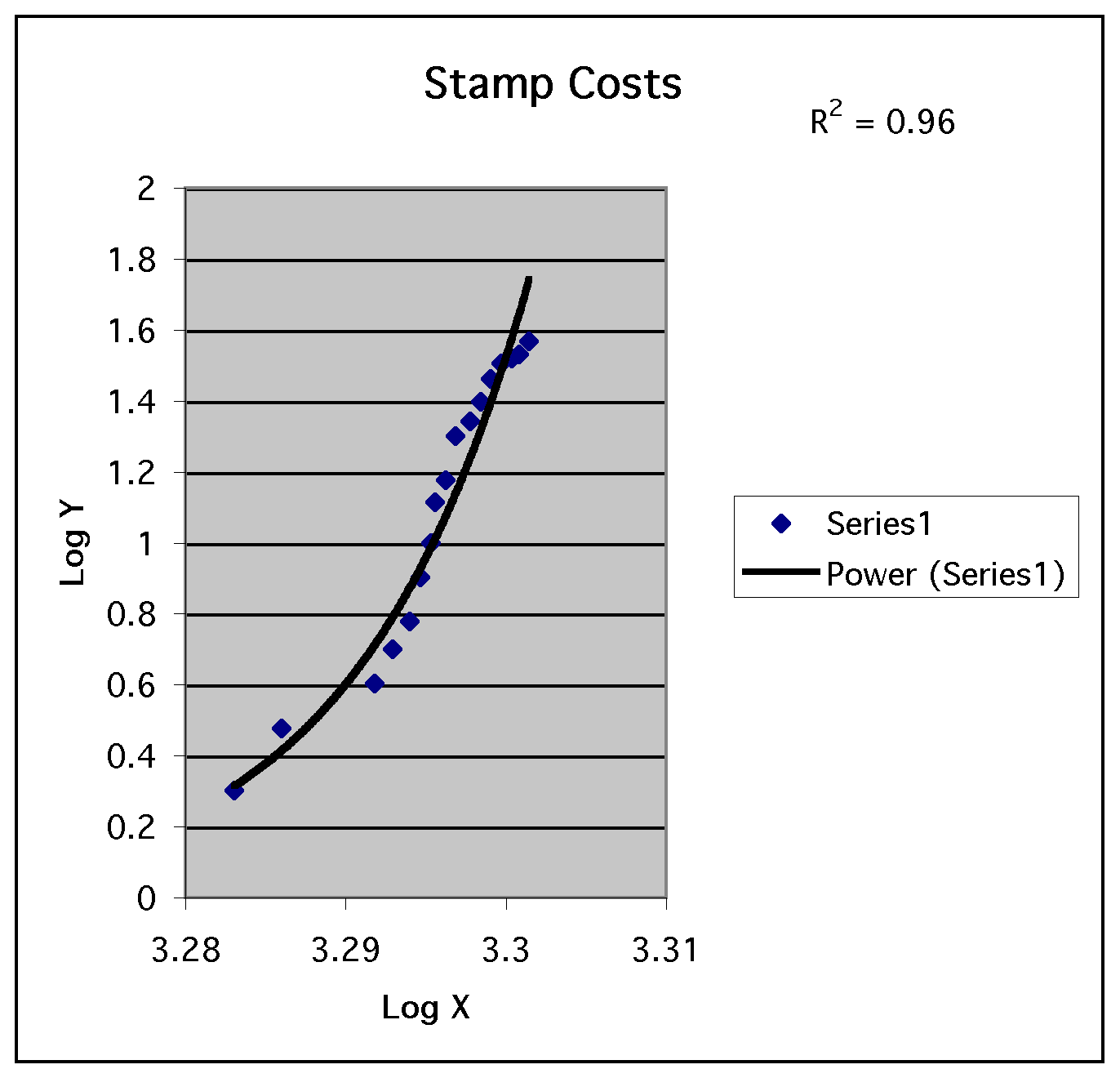
and we can use log x, log y as our ordered pairs to graph the points. The data we now have is

log x

log y
3.28307497473547 0.301029995663981
3.28600712207947 0.477121254719662
3.29181268746712 0.602059991327962
3.29292029960001 0.698970004336019
3.29402509409532 0.778151250383644
3.29468662427944 0.903089986991943
3.29534714833362 1
3.29556709996248 1.11394335230684
3.29622628726116 1.17609125905568
3.29688447553855 1.30102999566398
3.29776051109913 1.34242268082221
3.29841638006129 1.39794000867204
3.29907126002741 1.46239799789896
3.29972515397564 1.50514997831991
3.3003780648707 1.51851393987789
3.30081279411812 1.53147891704226
3.3014640731433 1.56820172406699

The graph below shows this data with the trend line added. The correlation coefficient is given as 0.96. The closer this correlation coefficient is to 1, the better it fits the function.

 

 

Now we can look at the exponential function along with the correlation coefficient.

We begin by using the form y = ab^x. If we again take the log of both sides, we have

log y = log (ab^x)

or

log y = log a + x log b

If we let log y = Y, log a = A, and log b = B, then we have Y = A + Bx. So now the equation again is linear. We will use x and log y to graph the data.

log y

x (year)
0.301029995663981 1919
0.477121254719662 1932
0.602059991327962 1958
0.698970004336019 1963
0.778151250383644 1968
0.903089986991943 1971
1 1974
1.11394335230684 1975
1.17609125905568 1978
1.30102999566398 1981
1.34242268082221 1985
1.39794000867204 1988
1.46239799789896 1991
1.50514997831991 1994
1.51851393987789 1997
1.53147891704226 1999
1.56820172406699 2002

 

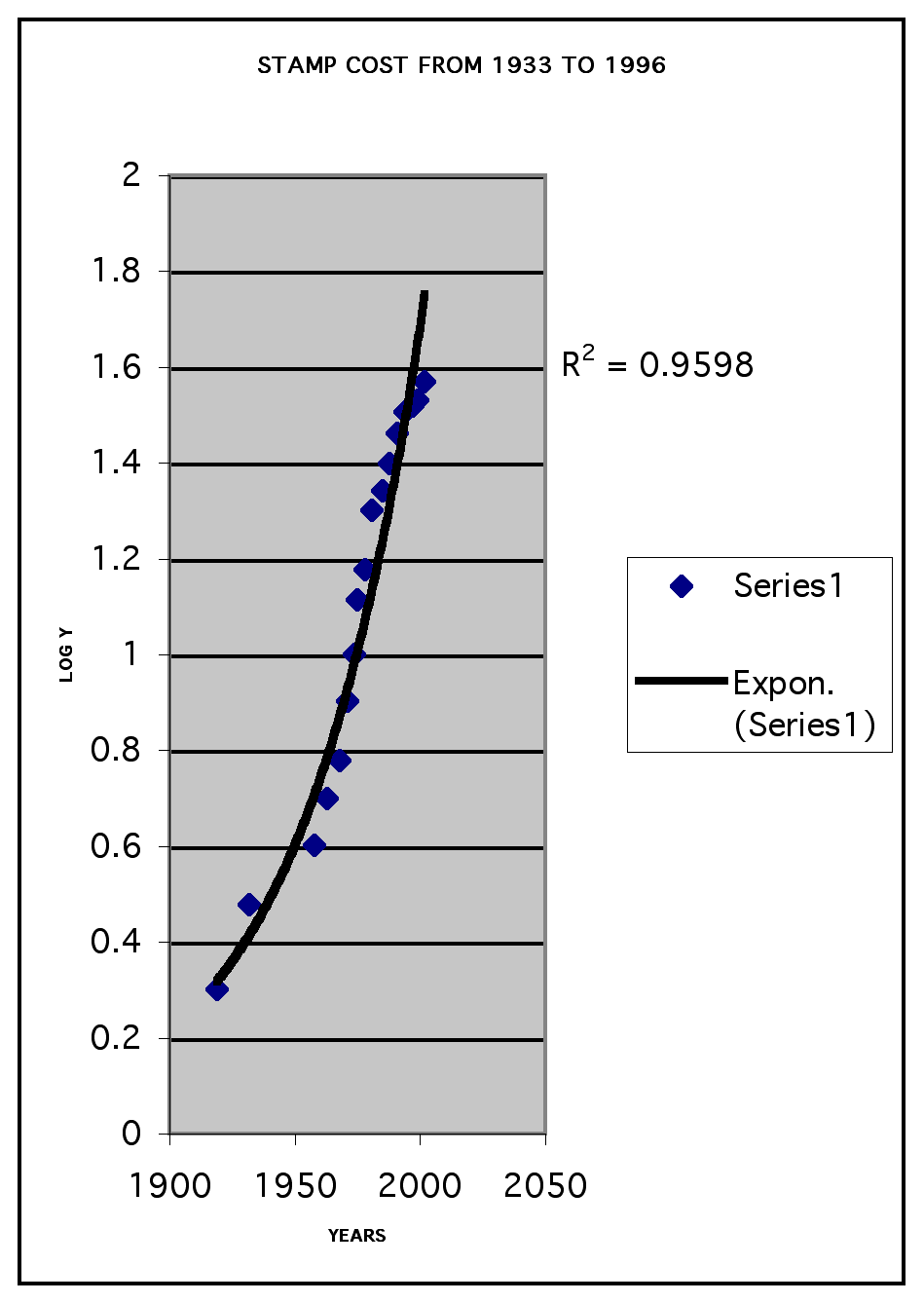
The correlation using the trend line is 0.9598. This is slightly less than the correlation coefficient given by the power function, but both are very close to 1 and both will give a good approximation of the trend.

So let's use the power function to predict the year that stamps will double in value? If they cost 0.37 in 2002, what year will they cost .74? When will they cost $1.00?

year rate(in cents) X1-Mean SQRED Y1-Mean SQRED
1919 2 -56 3136 -15.52 240.8704
1932 3 -43 1849 -14.52 210.8304
1958 4 -17 289 -13.52 182.7904
1963 5 -12 144 -12.52 156.7504
1968 6 -7 49 -11.52 132.7104
1971 8 -4 16 -9.52 90.6304
1974 10 -1 1 -7.52 56.5504
1975 13 0 0 -4.52 20.4304
1978 15 3 9 -2.52 6.3504
1981 20 6 36 2.48 6.1504
1985 22 10 100 4.48 20.0704
1988 25 13 169 7.48 55.9504
1991 29 16 256 11.48 131.7904
1994 32 19 361 14.48 209.6704
1997 33 22 484 15.48 239.6304
1999 34 24 576 16.48 271.5904
2002 37 27 729 19.48 379.4704
Total Sum Squared 8204 2412.2368
Divide by Sample 512.75 150.7648
Sx 22.6439837484485 Sy 12.2786318456089
Sx/Sy 1.84417808377784
SLOPE
POWER 1.77041096042673
EXPON. 1.77004212480997
Y-INTERCEPT
POWER 1943.98239997332
EXPON. 1943.98886197333

 

Using the information found in the above chart, we know that the equation y = 1.770x + 1943.98 will give us the value of stamps in any year.

Return to Phyllis' Home Page