For each of the following items, use a graphing program, such as Graphing calculator 3.2, or x function, to explore, understand, and extend. Prepare a file of discussion, summary or graphs to illustrate what you have found.
SELECT ONE PROBLEM TO WRITE UP AND POST YOUR WEBPAGE AS HOMEWORK
I have chosen to work on Question 5:
Examine graphs of y=asin(bx+c) for different values of a, b and c.
________________________________________________________________________________
Objectives of this Investigation:
1. To describe the graph patterns expected in sine models.
2. To interpret sine functions which are reflections across the x-axis, translations or stretches (or combinations of these transformtions )of basic functions.
Introduction
Situations where we model periodic change e.g. We live near Atlanta Ocean and we can track the depth of the water on a retaining wall every hour. We began recording the data at low tide at zero and we may eventually yield a set of data . We note that this change is periodic, i.e they change in regular patterns that repreat over constant intervals of time.
Basic Sine Curve
The basic sine curve repeats indefinitely to the right and left. We notice the following characteristics and keypoints:
1. Domain of the sine curve is the set of all real numbers
2. Range of the sine curve is the interval [-1,1]
3. Period of 2 p
4. The sine curve is symmetric with the origin
5. Intercepts
6. Maximum points
7. Minimum points
This means that y=sinx flips itself along the x-axis. In other words, y=-sinx is a mirror image along the x-axis of y=sinx.
We can rewrite our expression y=sin(-x) as y=-sin(x),which is a mirror image along the x-axis of y=sinx.
Vertical Stretch /shrink?
Let's examine y=asinx where a takes all values. the constant factor a acts as a scaling factor i.e. a vertical stretch or vertical shrink of the basic sine curve.
For absolute value of a > 1, the basic sine curve is stretched.
For absolute value of a <1, the basic sine curve is shrunk.
the result is that the graph of y-asinx ranges between -a and a instead of between -1 and 1.
The absolute value of a is the amplitude of the function y=asinx.
The range of the function y=asinx is
The following 3 examples illustrate vertical stretching and shrinking for a sine curve.
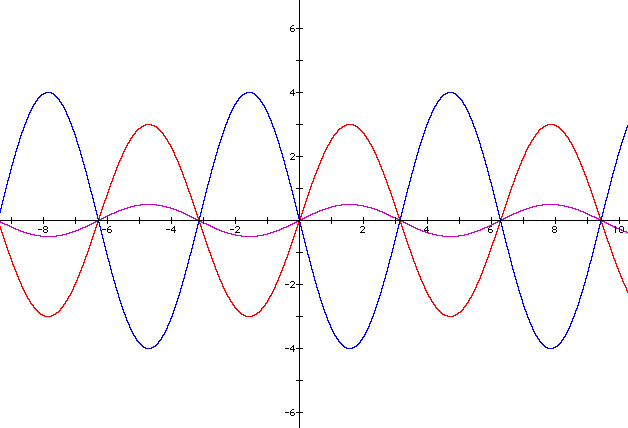
Horizontal Stretch /shrink?
Let y=asinbx where a takes all possible values and b is a positive real number.
The period of the basic sine curve is 2p, means one complete cycle happens between 0 and 2 p.
So,
completes half a cycle between 0 and 2 p and it completes one complete cycle between 0 and 4 p.
We generalize the above reasoning to find the period , T, of any sine curve as
Hence, we see that the sine curve sketch horizontally for 0 < b < 1.
Using similiar reasoning as above, for y=asinbx when b >1, suppose b=4, we have,
y=asin4x completing 4 cycles between 0 and 2 p. Thus, it completes one complete cycle between 0 and 1/2 p.The sine curve shrinks horizontally whenever b > 1.
We can rewrite the expression y=sin(-bx) as y=-sinbx which is discussed earlier.
Click ME to open graphics calculator. Change the limits of b to explore.
What about y=asin(bx+c) ?
We now examine the full expression y=asin(bx+c) where c is a constant.
Let's compare y=asinbx with y=asin(bx+c).
The graph of y=asinbx completes one cycle in bx.
The graph of y=asin(bx+c) completes one cycle in bx+c in th range (0,2p) i.e.
Solving these 2 equations yield,
and
Hence, the interval for one cycle has to be
Click me to see an illustration.
What happens when c < 0 ?
We have, y=asin(bx+c) = asin(bx-c) ,
The graph of y=asin(bx-c) completes one cycle in bx-c in th range (0,2p) i.e.
and
Hence, the interval for one cycle has to be
This implies that y=asinbx
is shifted by an ![]() amount to the right
on the axis.
amount to the right
on the axis.
Summary of investigation
|
|
|
|
|
| Positive |
|
|
|
| Negative |
|
|
|
|
Less than 1 Bigger than zero |
|
|
|
Further Investigation
We can organize our thinking about functions in terms of families whose members share symbolic rules tht are like graphs that have a chracteristic shape and tables that display similar patterns. Examples of some types of functions are; linear, quadratic, inverse power, exponential, trigonometric, absolute value and sqaure root. We can adjust the algebraic rules of the basic function types to match graphs that are related to one of the basic function graphs by the following transformation:
(1) Vertical translation by f(x) + c
(2) Vertical stretching or compression by af(x)
(3) Horizontal translation by f(x+b)
(4) Horizontal stretching or compression by f(ax)
(5) Reflection across the x-axis is -f(x)