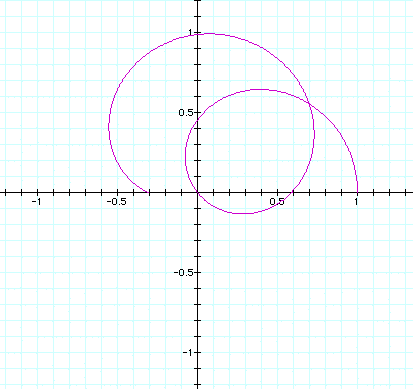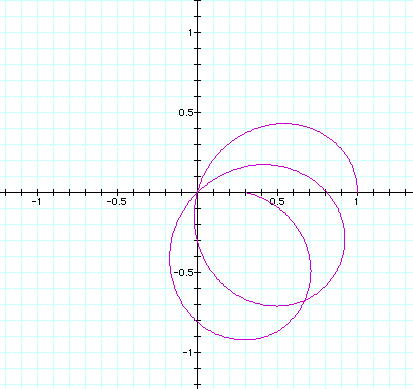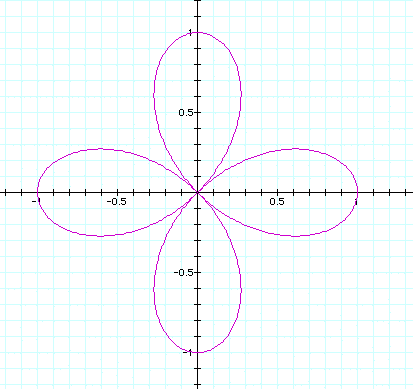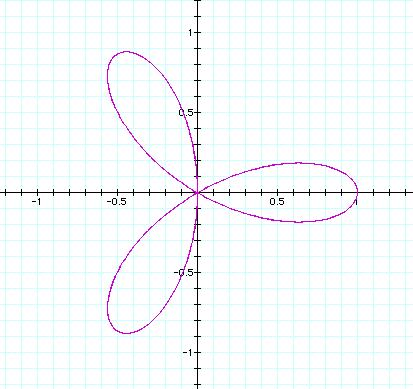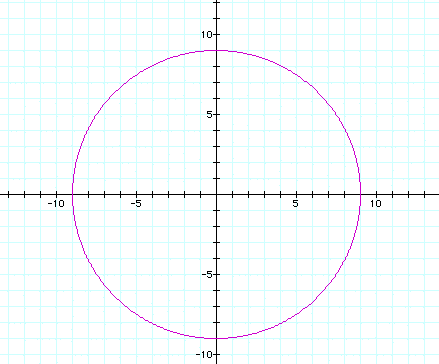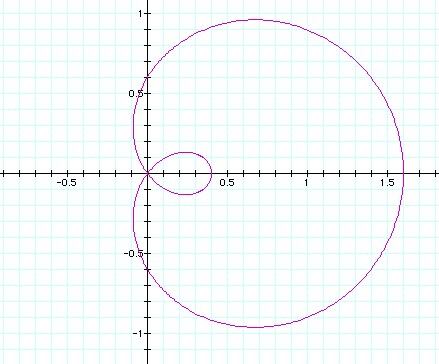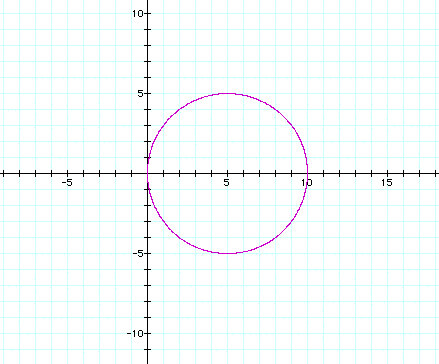Polar Equations
The following equation will be
investigated:
r = a + b cos (kJ)
The first several graphs have a fixed at 0, b = 1 and variations
with n: 0+ 1*cos(nq).
n = .01
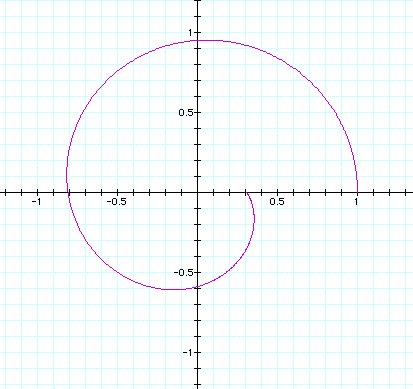
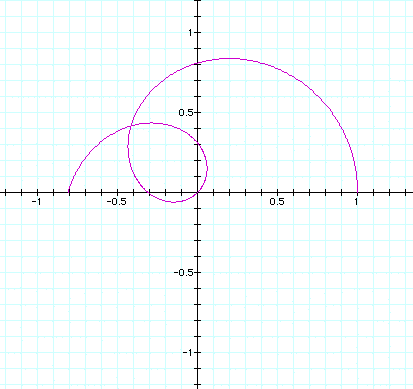
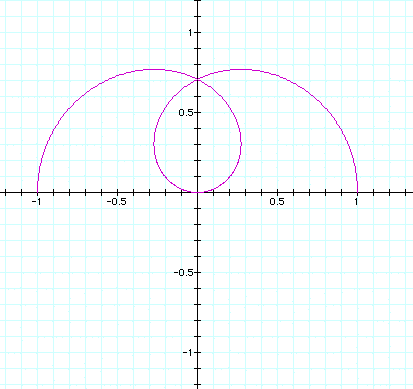
 n varies from > .01 to < 1.0 in the next 4 pictures.
It shows how the circle at n = .01 'breaks' apart and begins to
form 'loops', then recombines to form more than one circle at
n = 1.
n varies from > .01 to < 1.0 in the next 4 pictures.
It shows how the circle at n = .01 'breaks' apart and begins to
form 'loops', then recombines to form more than one circle at
n = 1.
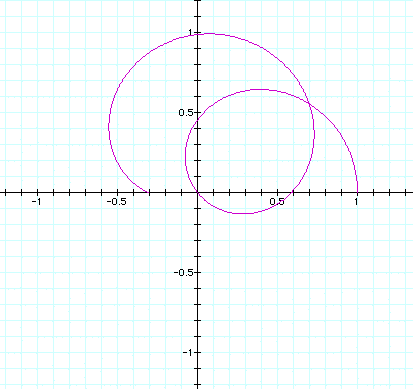 n = 1
n = 1
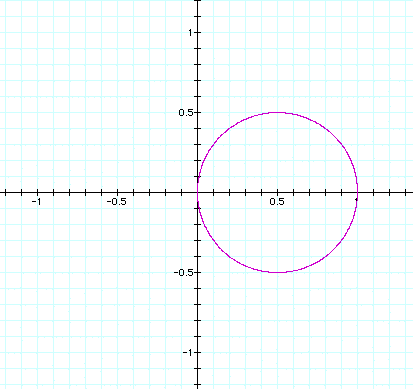 As n increases, the circles at n = 1 split apart and
form lobes.
As n increases, the circles at n = 1 split apart and
form lobes.
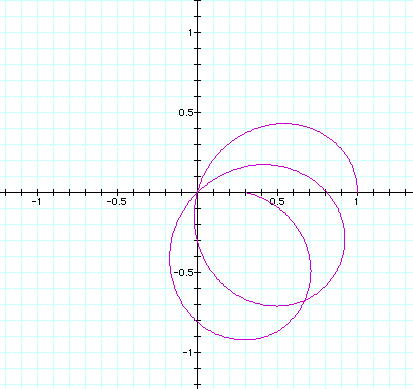 n = 2 here, notice that with n = 2 , you get 4 lobes;
what is interesting is...
n = 2 here, notice that with n = 2 , you get 4 lobes;
what is interesting is...
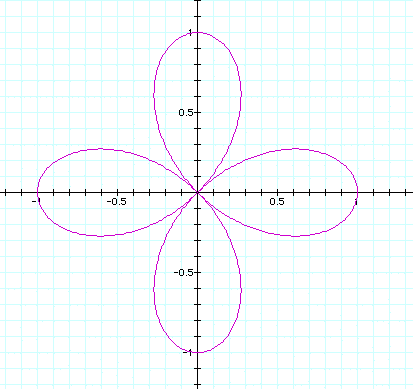 ...at n = 3, there are 3 sets of 2 lobes superimposed,
not 3 lobes. Because...
...at n = 3, there are 3 sets of 2 lobes superimposed,
not 3 lobes. Because...
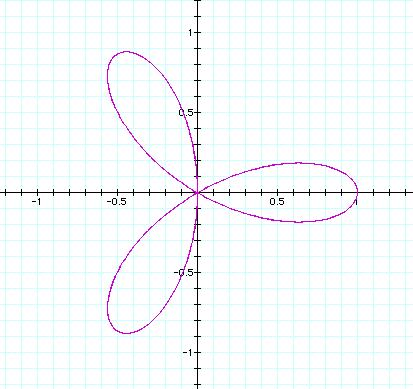 as we will see, with
an even number the pattern is 2n. Now, at n = 4 the result is
8 lobes or 2n lobes.
as we will see, with
an even number the pattern is 2n. Now, at n = 4 the result is
8 lobes or 2n lobes.
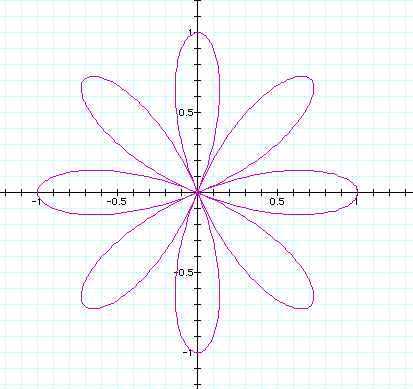 Here n = 9 (double lobes).
Here n = 9 (double lobes).
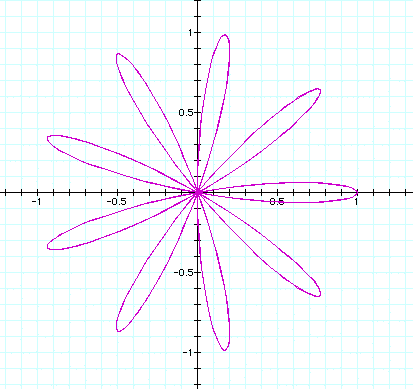 Finally, n = 10 with the result of 20 lobes (2n lobes).
Finally, n = 10 with the result of 20 lobes (2n lobes).
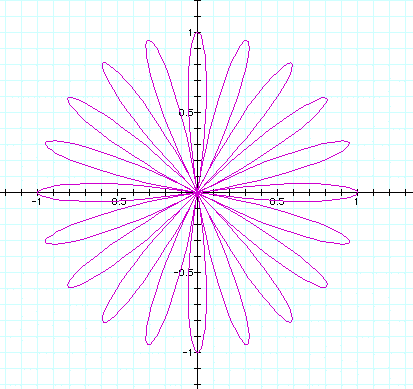 It is interesting that when n varies from -10 to -.01
that one obtains the identical results in each case as those above.
************************************************************
This equation is: 1 + 1*cos(n*q),
with n beginning with 1. The following graphs occur when n moves
from 1 to 10:
It is interesting that when n varies from -10 to -.01
that one obtains the identical results in each case as those above.
************************************************************
This equation is: 1 + 1*cos(n*q),
with n beginning with 1. The following graphs occur when n moves
from 1 to 10:
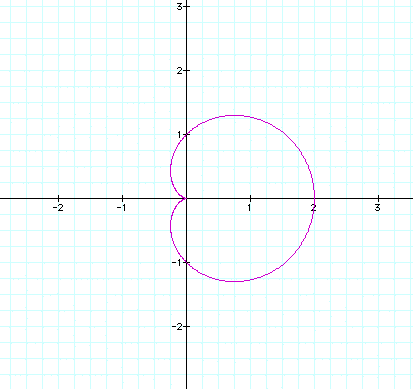 n = 2:
n = 2:
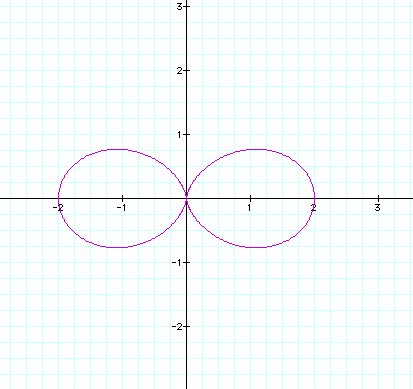 n = 7:
n = 7:
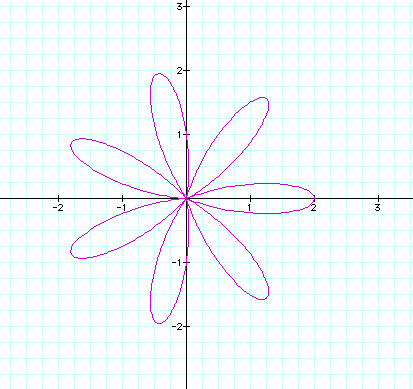 n = 8; There is 1 lobe for every increment of n (1n
= # lobes). Again, this was for 1 + 1*cos(nq).
n = 8; There is 1 lobe for every increment of n (1n
= # lobes). Again, this was for 1 + 1*cos(nq).
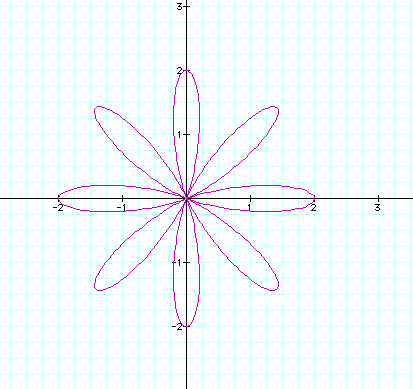 When the values for n vary from -10 to 0, the identical
results occur as above.
*******************************************************
The next series begins (and ends quickly) with
a + 1*cos(0*q):
When the values for n vary from -10 to 0, the identical
results occur as above.
*******************************************************
The next series begins (and ends quickly) with
a + 1*cos(0*q):
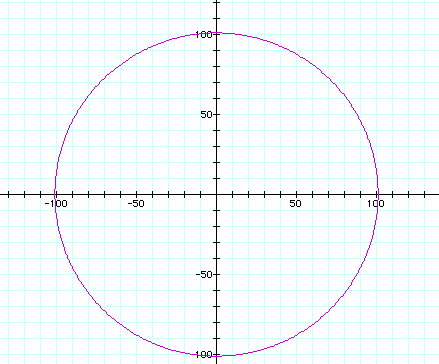
As a increases from 0 to 100 with 1*cos(0), [of course,
cos(0) = 1],the figure remains a circle with a diameter that equals
2a + 2 , therefore, a + 1 = the radius. Here, a = 10:
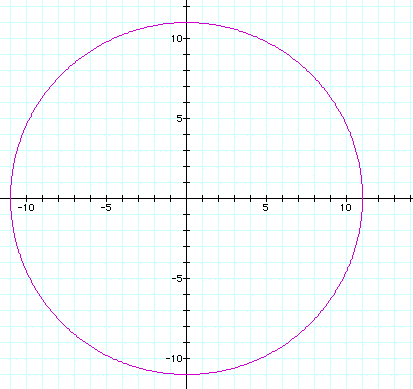 a = 100:
a = 100:
 When n varies from -10 to 0, the result are circles;
when n = -1 the circle disappears as expected; when n < 0,
r = a + 1 but with a diameter of 2 less than circles with n >
0. Here n = -10:
When n varies from -10 to 0, the result are circles;
when n = -1 the circle disappears as expected; when n < 0,
r = a + 1 but with a diameter of 2 less than circles with n >
0. Here n = -10:
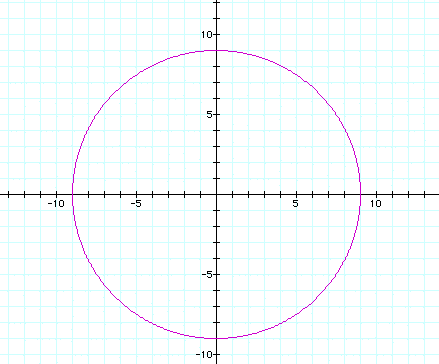 *****************************************************************
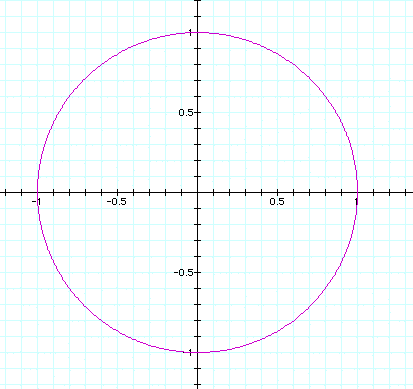
This series is for r = n + 1 cos(1q)
When n = 0, the figure is a circle; a cardioid when
n = +/-1; For -1 < n < 0 and 0 < n < 1 the type of
figure is :
*****************************************************************
This series is for r = n + 1 cos(1q)
When n = 0, the figure is a circle; a cardioid when
n = +/-1; For -1 < n < 0 and 0 < n < 1 the type of
figure is :
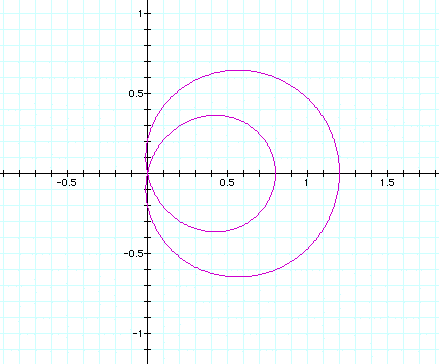 For the above graph, n = +/- .2; below, n = +/- .6:
For the above graph, n = +/- .2; below, n = +/- .6:
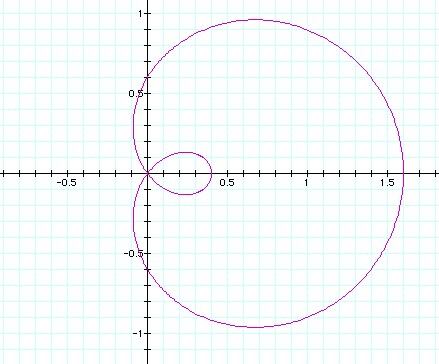 The figure inside the larger circle is 'moving out'
from the inside, making a cardioid at n = +/- 1 and then forming
a circle (proper) at n = 3. Up to n = 3 it is still an imperfect
'looking' circle.
For the series of r = 0 + n cos (1q),
when n = 0 there is no circle of course, but for n > 0, a circle
forms such that its left side stays fixed at (0,0). For n <
0 the figure is a circle but it is fixed on its right side at
(0,0):
The figure inside the larger circle is 'moving out'
from the inside, making a cardioid at n = +/- 1 and then forming
a circle (proper) at n = 3. Up to n = 3 it is still an imperfect
'looking' circle.
For the series of r = 0 + n cos (1q),
when n = 0 there is no circle of course, but for n > 0, a circle
forms such that its left side stays fixed at (0,0). For n <
0 the figure is a circle but it is fixed on its right side at
(0,0):
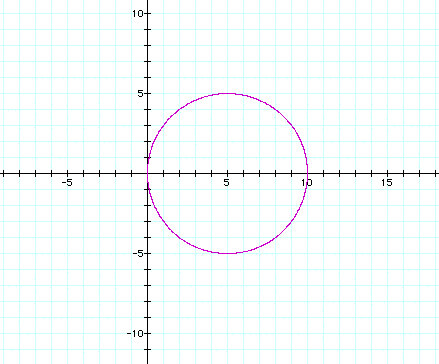
 Finally, with the series of r = 1 + n cos (1q),
a circle is formed at n = 0, a cardioid at n = 1, for n > +1
or n < -1, a circle forms from the cardioid and gets larger
inside a larger circle:
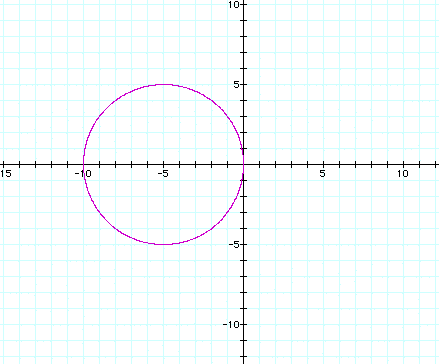
Finally, with the series of r = 1 + n cos (1q),
a circle is formed at n = 0, a cardioid at n = 1, for n > +1
or n < -1, a circle forms from the cardioid and gets larger
inside a larger circle:
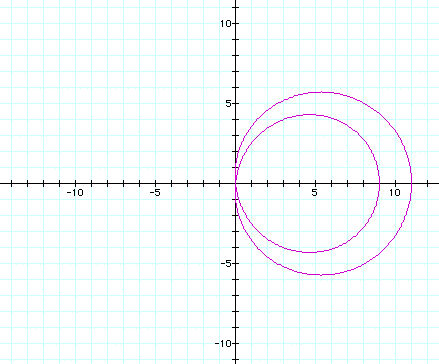
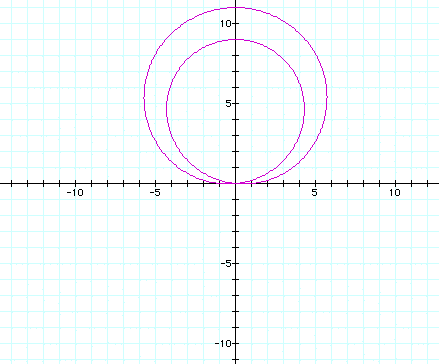
 It is interesting that both circles are fixed at (0,0)
and the 'outside' edge of the inner circle versus the outer circle
are 2 units apart consistently (even when n = 100). Here, the
inner circle reaches -9 and the larger circle reaches -11 (n-1
and n+1 for values of n).
When cos is replaced by sin in the preceding graphs
the circles are oriented 90 degrees versus the previous graphs.
With n > 0, the double circles are on top of the x axis and
under the x axis with both circles fixed at (0,0).
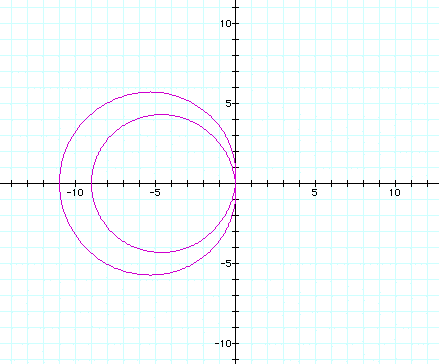
It is interesting that both circles are fixed at (0,0)
and the 'outside' edge of the inner circle versus the outer circle
are 2 units apart consistently (even when n = 100). Here, the
inner circle reaches -9 and the larger circle reaches -11 (n-1
and n+1 for values of n).
When cos is replaced by sin in the preceding graphs
the circles are oriented 90 degrees versus the previous graphs.
With n > 0, the double circles are on top of the x axis and
under the x axis with both circles fixed at (0,0).
 Further investigations are left up to the reader.
Further investigations are left up to the reader.
Return to home page