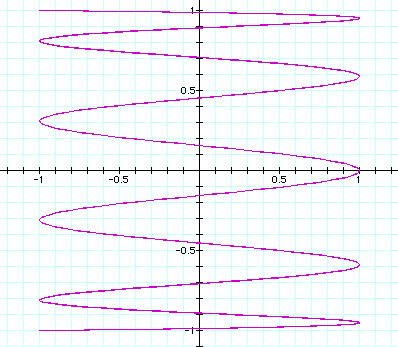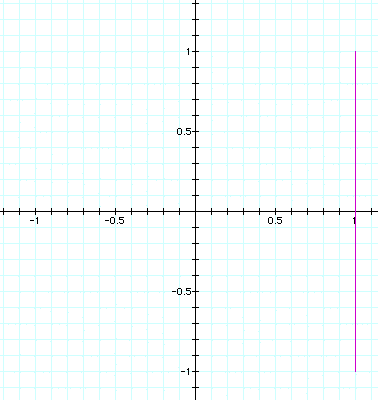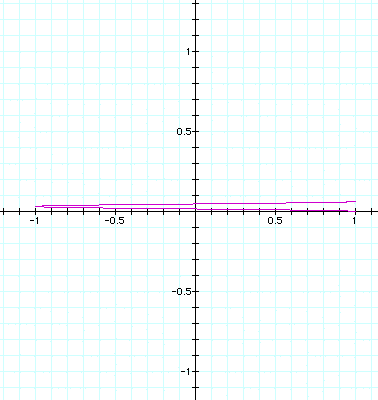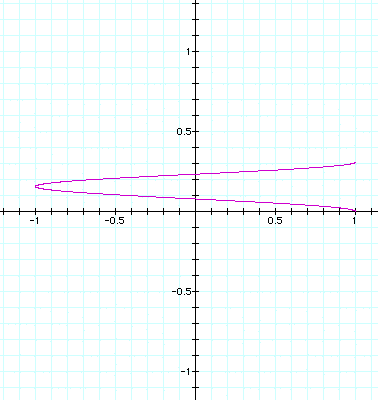Parametric Curves of Sin and Cosine
I will be investigating the parametric curves of the
form x = cos(at) and y = sin(bt) for various values of a and b.
For all of the following curves, 0< t<2p
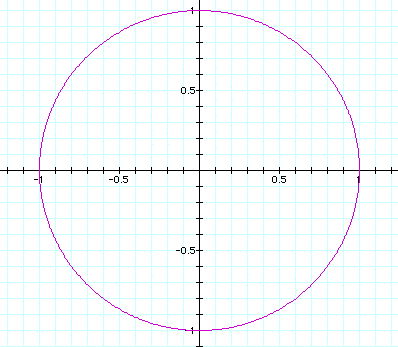
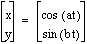 a = 1, b =1
a = 1, b =1
This figure shows that the graph travels through one exactly;
not only here but at +/-1 and on both axes.
The next two figures have a and b interchanged with
the values of 10 and 1:
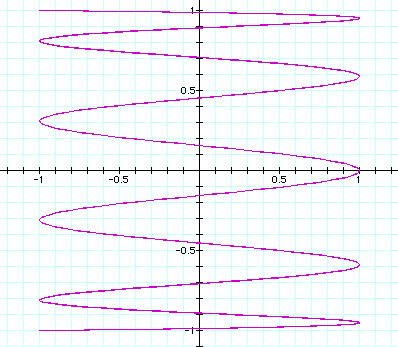 a = 10, b = 1
a = 10, b = 1
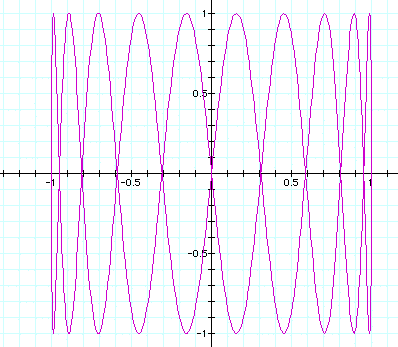 a = 1, b = 10 (above)
When both are equal to ten, the 'circle' has a definite
thickness that is well illustrated in the figure after this one:
a = 1, b = 10 (above)
When both are equal to ten, the 'circle' has a definite
thickness that is well illustrated in the figure after this one:
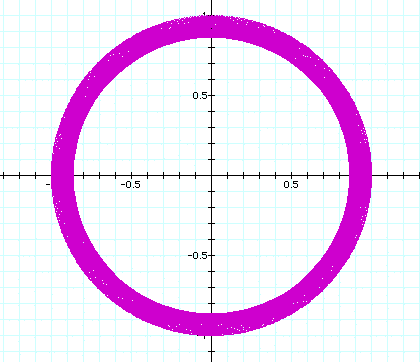
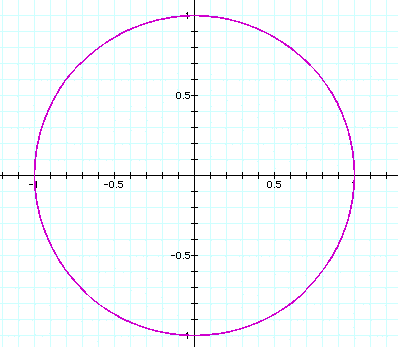 a = b = 10
Close up of the above graph:
a = b = 10
Close up of the above graph:
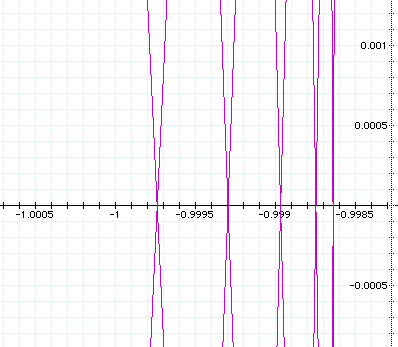 Here is the 'thickness' of the circle illustrated as
one of its characteristics.
For a = 100, b = 1 (below):
Here is the 'thickness' of the circle illustrated as
one of its characteristics.
For a = 100, b = 1 (below):
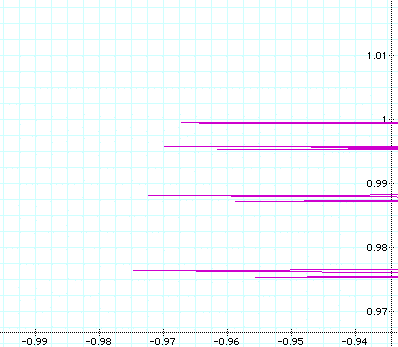 The spear-like projections are evident here and in
the next picture:
The spear-like projections are evident here and in
the next picture:
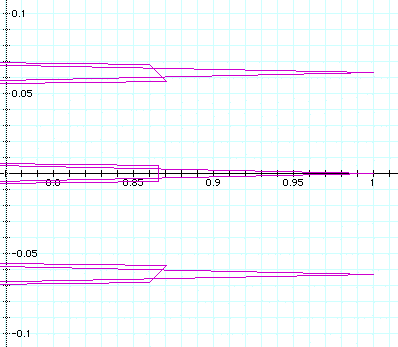 Notice the symmetry of the middle lines of the top
and bottom 'spikes'. Both are pointing toward the x axis. The
middle line is vertical only on the axis.
Below, a = 1, b = 100:
Notice the symmetry of the middle lines of the top
and bottom 'spikes'. Both are pointing toward the x axis. The
middle line is vertical only on the axis.
Below, a = 1, b = 100:
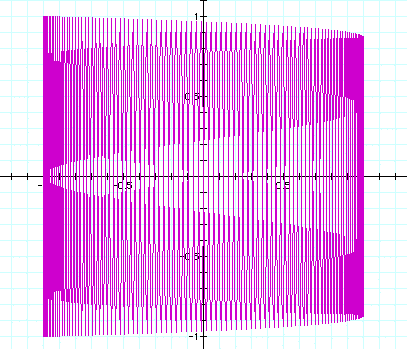 When the values for a and b are 'switched' the pointed
sides rotate 90 degrees.
When the values for a and b are 'switched' the pointed
sides rotate 90 degrees.
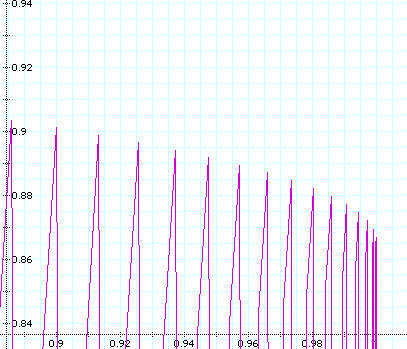 The points ascend to 1 eventually, and only toward
the left side; The spikes on the bottom ascend to -1 on the left
side as well:
The points ascend to 1 eventually, and only toward
the left side; The spikes on the bottom ascend to -1 on the left
side as well:
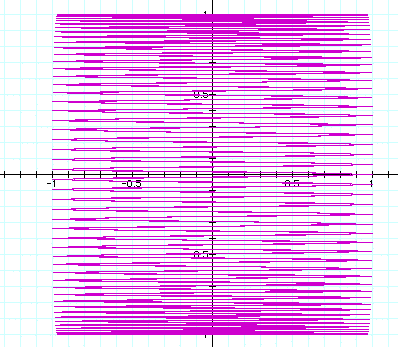
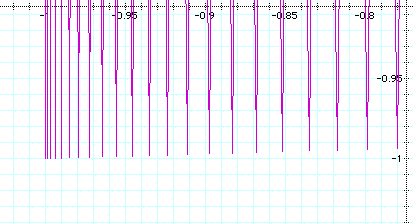 a = 100, b = 100:
a = 100, b = 100:
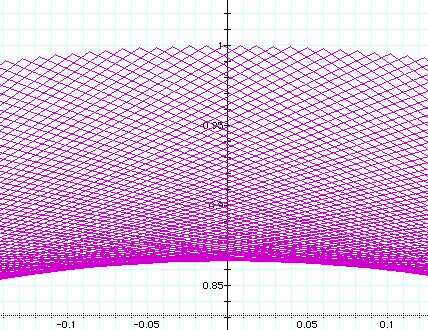
 Note the symmetrical property of the 'mesh' or net:
Note the symmetrical property of the 'mesh' or net:
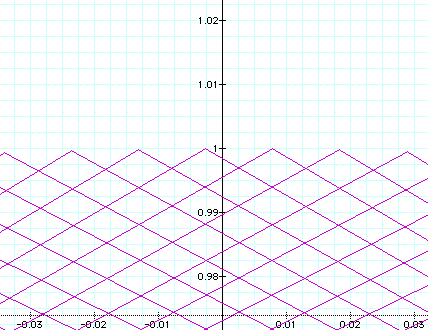
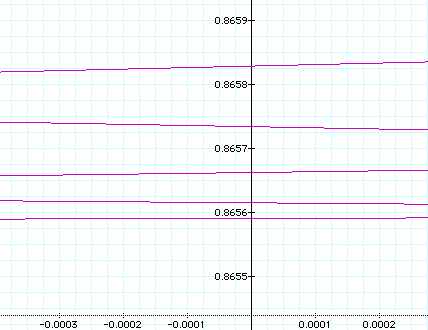
 a = 1000, b = 100:
a = 1000, b = 100:
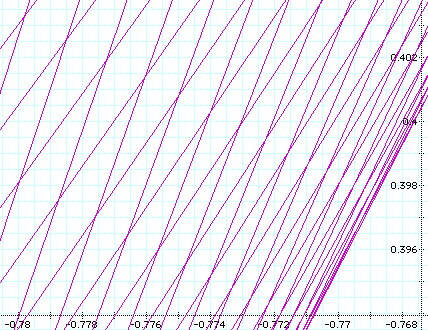
 This is a very unique design; the boundaries are very
interesting.
This is a very unique design; the boundaries are very
interesting.

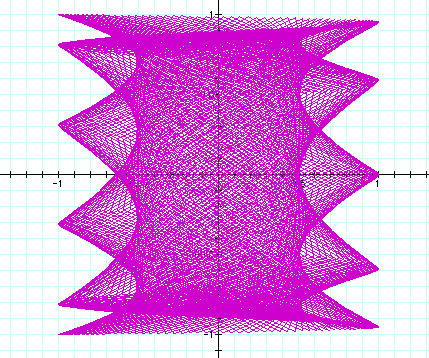
 Now, as the values become smaller the design is less
ornate:
a = .01, b = 1:
Now, as the values become smaller the design is less
ornate:
a = .01, b = 1:
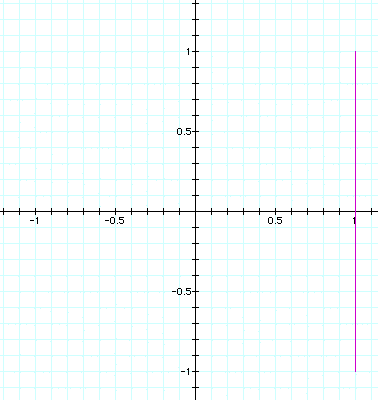 a = .05, b = 1:
a = .05, b = 1:
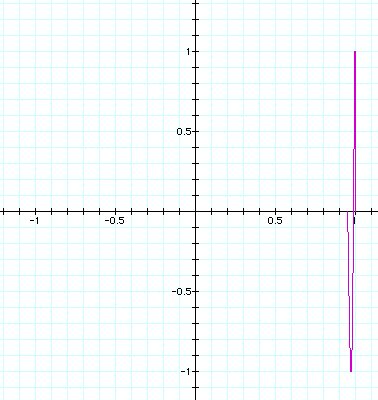 Below, a = 0.1, b = 1:
Below, a = 0.1, b = 1:
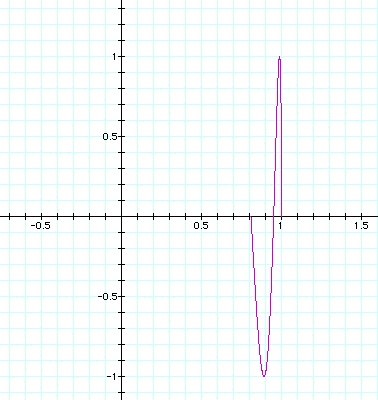 a = 0.5, b = 1, below:
a = 0.5, b = 1, below:
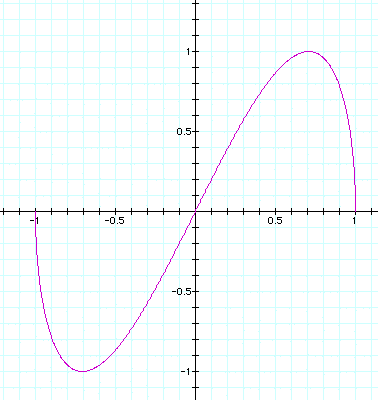 a = .9, b = 1, below:
a = .9, b = 1, below:
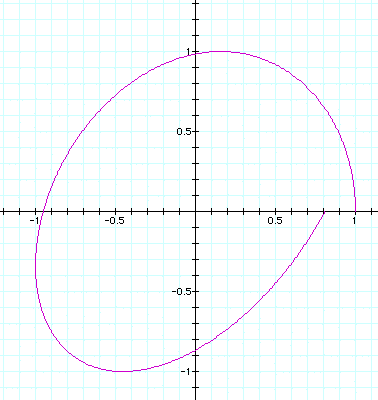 a = .98, b = 1:
a = .98, b = 1:
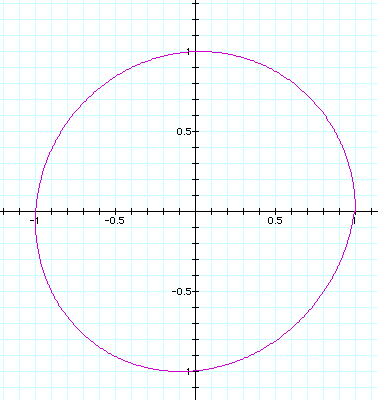 a = 1, b = .01:
a = 1, b = .01:
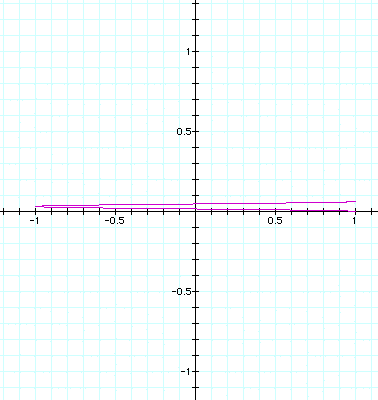 a = 1, b = .05:
a = 1, b = .05:
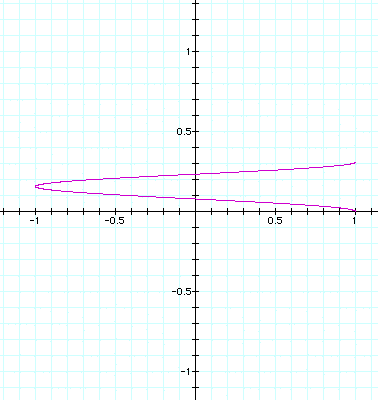 a = 1, b = .09:
a = 1, b = .09:
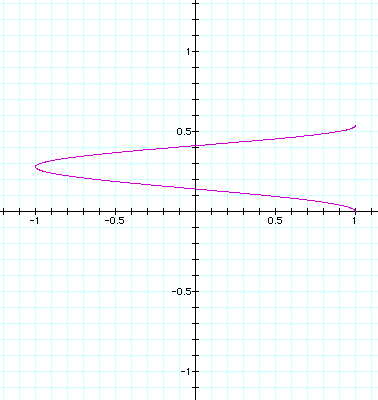
a = 1, b = -.09; Note, with b = -.01 and -.05 the graphs are
like those above with the exception that they are located below
the horizontal axis as below:
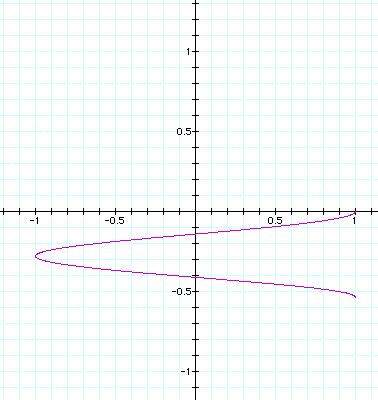
When a = b = -.01, -.05 respectively, the graph is of a much
shorter curve falling below the horizontal axis at 1 and moving
down. Here is where a = b = -.09:
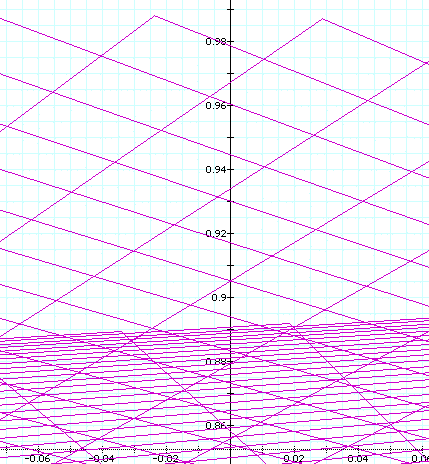
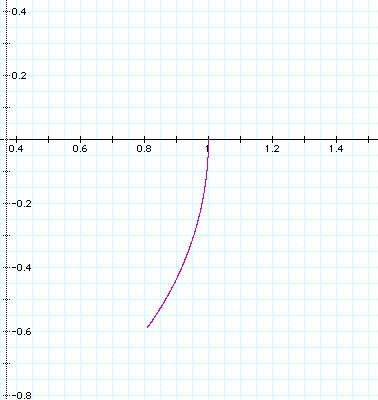 There is a great deal going on that needs much more
attention in future work.
There is a great deal going on that needs much more
attention in future work.
Steve's Home Page