

The third fallacious proof is:
Consider triangle ABC, with MN parallel to BC and MN intersecting AB and AC in poins M and N, respecitvely.
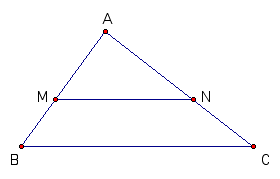
We will now prove that BC = MN.
Because MN is parallel to BC, we have triangle AMN ~ triangle
ABC and BC/MN = AB/MN.
It then follows that:
Now, multiply both sides of this equality by (BC - MN) to get:
By adding (BC)(AM)(MN) - (AB)(MN)(BC) to both sides, we get:
This equation can be written as:
No discussion of mathematical fallacies would be complete without an example of a dilemma from division by zero. We committed this mathematical sin when we divided by zero in the form of [(BC)(AM) - (AB)(MN)], which was a consequence of the triangles proved to be similar earlier.