Here is the answer to the challenge
problem of Lesson 2 Day 2:
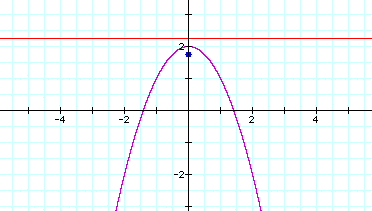
The function is y = -x^2 +2.
The focus for this parabola is (0,1.75) with
directrix y= 2.25:
Here is a close up showing how one
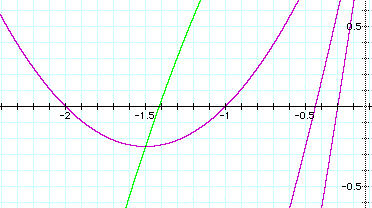
arm of -x^2 + 2 passes through the minimum point:
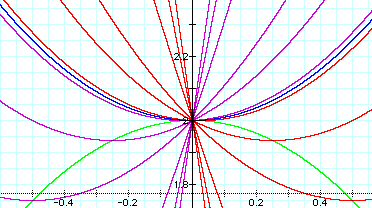
This picture is that of the parabola
at its' maximum point at (0,2):
Click HERE
to see the movement of ax^2 + bx + c with respect to time.
Try to identify which moving graph corresponds to the three variations
of ax^2 + bx + c that was discussed. To start the movie, click
on the lower left arrow; To close, click on the upper left box.
I believe for demonstration, if 5 graphs
were produced then careful explanation is required to avoid any
confusion. If 1 graph at a time were demonstrated, one would need
an explanation for each one and then a summary of all the graphs
to avoid confusion. In all cases, an explanation is essential.
Back to previous page
Back
to main conics page