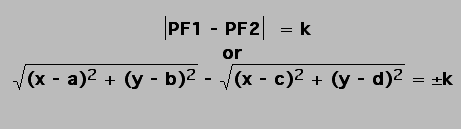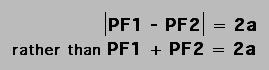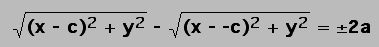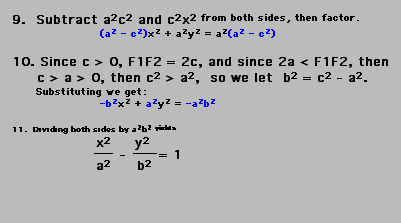Information Section:

This information section objectives are:

1. State and apply properties of hyperbolas to draw be able to draw or describe them.

2. Allow the student to use properties of hyperbolas to write equations describing them.

Dandelin Spheres and the Hyperbola

Dandelin presents a way of looking at the three-dimensional definition of a hyperbola as a conic section and relating it to a two-dimensional definition in terms of foci and focal constant. This is not very much different than the approaches he took for the ellipse/circle. (Lesson 3)

Consider a hyperbola formed by a plane M intersecting both nappes of a cone.

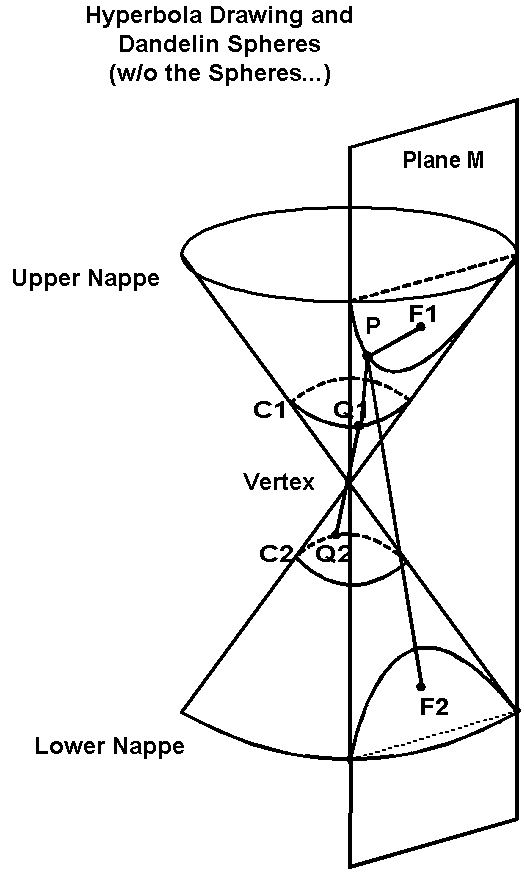
As was shown with the ellipse, two spheres (S1 and S2) are tangent to the cone and to the plane M. (one in each nappe). Let F1 and F2 be the points of tangency of the speres with the plane and C1 and C2 be the circles of intersection of the spheres and the cone.

There is a property that relates any point P on the hyperbola to the fixed points F1 and F2. Suppose P is on the nappe of the cone containing sphere S1. P is on the line PV of the cone. Line PV will also intersect the circles C1 and C2 at points Q1 and Q2, respectively. Note that Q1Q2 is the distance along the edge between the circles C1 and C2. Also note that the circles lie on parallel planes. This means that the distance between Q1 and Q2 (Q1Q2) is constant independent of the position of P.

Now notice that line segment PF1 and PQ1 are tangents to sphere S1 from point P. Also, line segments PF2 and PQ2 are tangents to sphere S2 from point P. Therefore:

PF1 = PQ1

and

PF2 = PQ2.

It follows that:

PF2-PF1 = PQ2-PQ1 = Q1Q2 (which is constant)

That means that PF2 - PF1 is also constant.

If P were located on the nappe of the other cone, then the argument would result in:

PF1 - PF2 = PQ1 - PQ2 = Q1Q2...

the same constant as above.

Since either PF1-PF2 or PF2-PF1 = Q1Q2, then

| PF2 - PF1 | = Q1Q2

This property is normally taken as the two-dimensional definition of a hyperbola.

A Two-Dimensional Definition of the Hyperbola

Theorem and Proof

Definition:

Let F1 anf F2 be two given points in a plane and k be a positive real number with k < F1F2. Then the hyperbola with foci F1 and F2 and focal constant k is the set of all points in the planes which satisfy | PF1 - PF2 | = k.

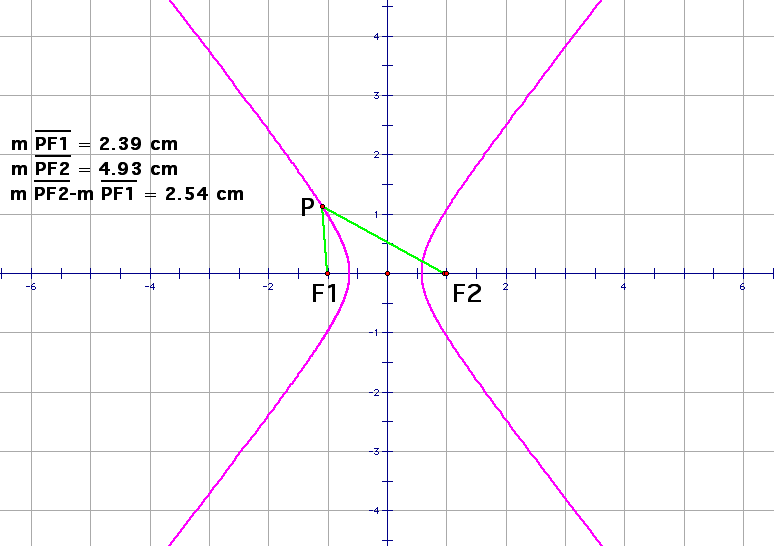
In the example below, the hyperbola shown has foci (F1 and F2) that are 2 units apart and k = 2.54. Notice that unlike the ellipse, the hyperbola is unbounded. A point can be farther than any specificed distance from either focus, and still be 2.54 units closer to one focus than the other.

Hyperbolas have the same symmetries as ellipses.

Theorem:

A hyperbola with foci F1 and F2 is a reflection-symmetric to line F1F2 and to the perpendicular bisector of the line segment F1F2.

(Picture)

Proof: This follows the same logic shown in the corresponding proof for the ellipse, found in (Lesson 3). One need only replace the references of PF1 + PF2 = k with |PF1 - PF2 | = k to complete the proof.

Developing an Equation for a Hyperbola

Explanation:

From the two-dimensional definition of the hyperbola, an equation for any hyperbola in the plane can be found. A similar method as was used with the ellipse can be used.

If the foci are F1 = (a,b) and F2 = (c, d) and the focal constant is k, then any point P = (x, y) on the hyperbola must satisfy the equation:

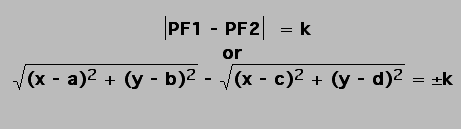
This is an equation for the hyperbola. It appears to be unweildly and does not lend itself to graphing. (even using Graphing Calculator, or other graphing tools). If we choose our foci well, we may be able to find a less cumbersome equation for the hyperbola. We can apply transformations to generate equations for other hyperbolas.

 

Theorem (Equation for a Hyperbola)

By choosing foci at (c, 0) and (-c, 0) and a focal constant of 2a we can yield the following equation for the hyperbola:

Proof:

The proof is identical to proof for an ellipse, in standard form, with two exceptions.

In Step 1, the definition of the hyperbola is:

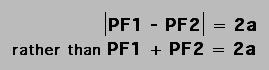
Also in step 1, if P = (x, y), F1 = (c, 0) and F2 = (-c, 0), then using the distance formula...

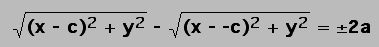
Steps 2 through 9 are then identical as those shown for the ellipse.

In Step 10, there is another difference:

This accounts for the minus sign in the equation for the hyperbola, where there is a plus sign for the ellipse.

The complete proof is also provide here below...

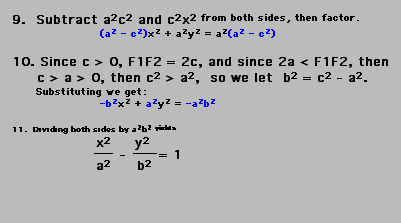
Investigation Section

Activity 1 - Technology Connection

The following presents how the hyperbola changes graphically, as we change items from the standard equation. Animation is provided in the examples shown below, where each of the parameters within the equation are changed within a given range.

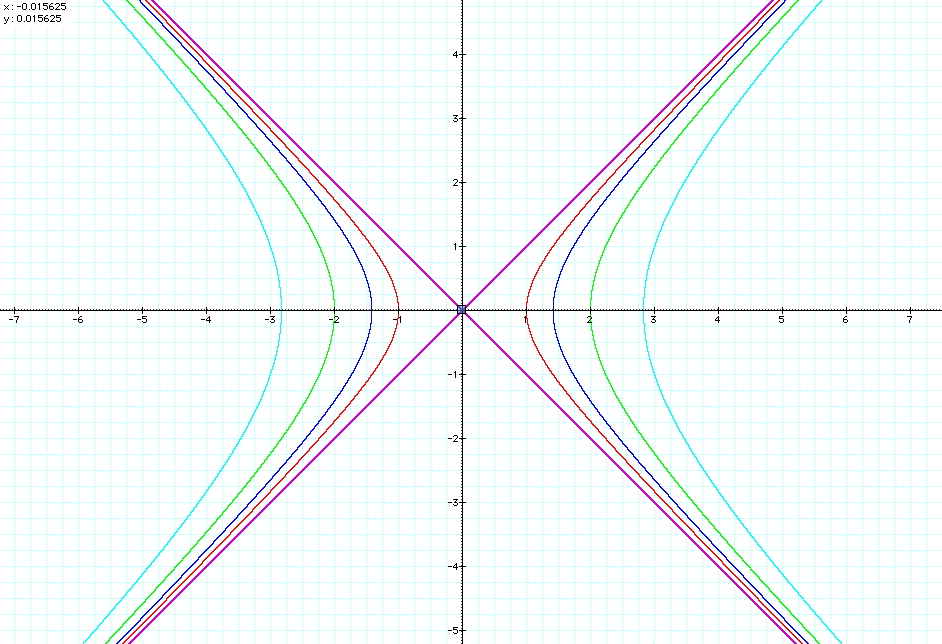
The affects of changing the "k" value is shown above for k = 0, 1, 2, 4, 8

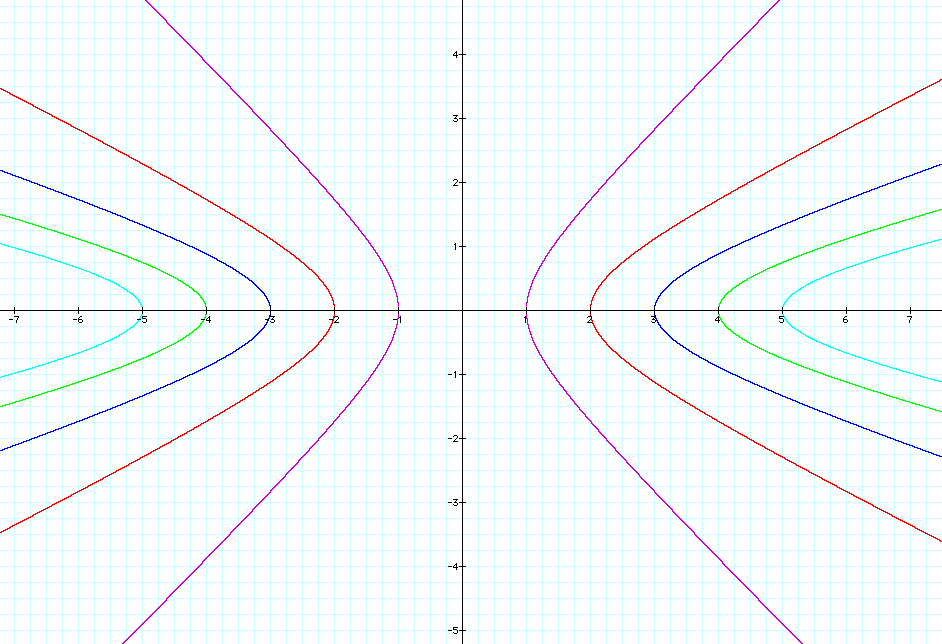
The affects of changing the "a" value is shown above for a = 1, 2, 3, 4, 5

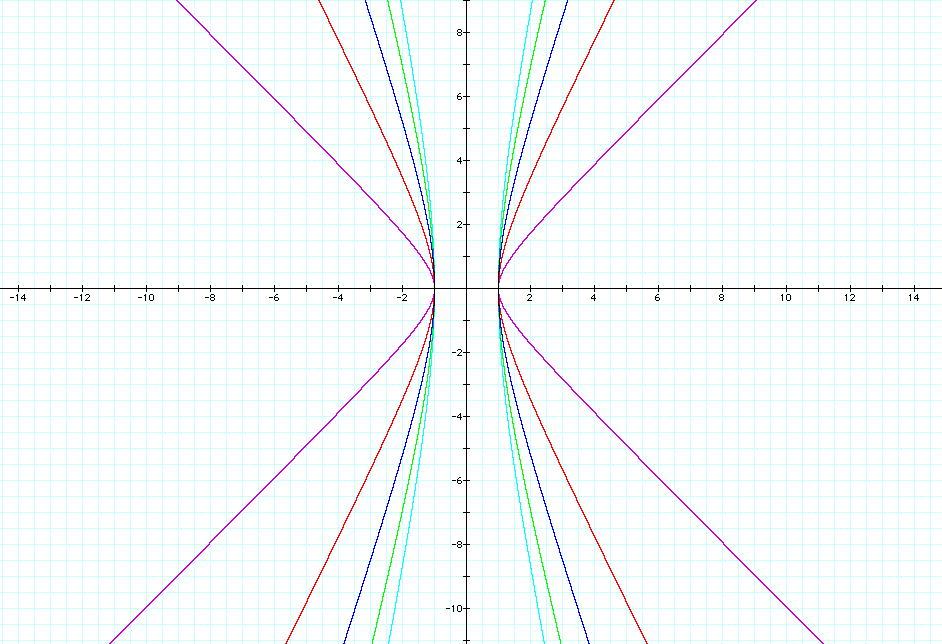
The affects of changing the "b" value is shown above for b = 1, 2, 3, 4, 5

Lesson 4 Day 1 Activity - Graphing Calculator File

If you have the Graphing Calculator application on your computer, you can use the link above to work with the file and further investigate the equation for the hyperbola.

Return to Lesson 4, Day 1 Page