Information Section:
This information section objectives are:
1. Be able to graph or identify graphs of hyperbolas given their equations.
2. Be able to graph transformation images of parent hyperbolas.
The Simplest Equation form of Hyperbola

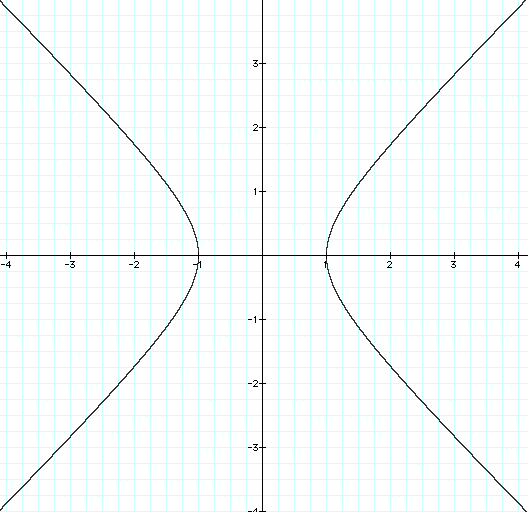
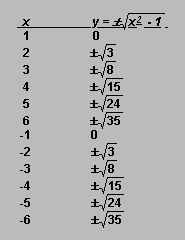

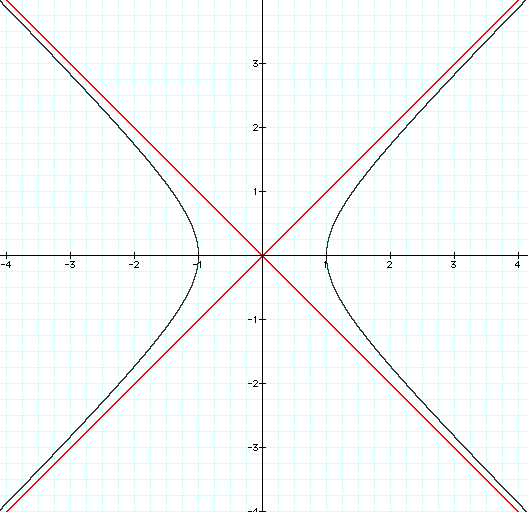

With a scaling +/-4 --------------------------------------------vs. +/- 15
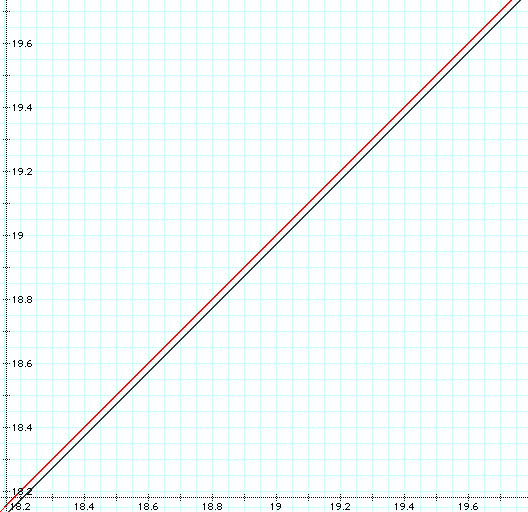
Showing that the asymptote and hyperbola do not intersect, as we extend out from the origin.
The Hyperbola:

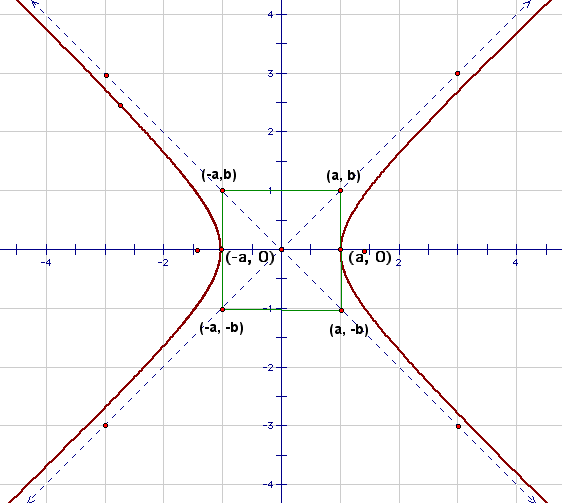
Each asymptote contains the origin. One asymptote goes through the points (a, b) and (-a, -b); the other goes through (a, -b) and (-a, b). Drawing the rectangle with these four points as vertices and the lines determined by its diagonals, helps to position the hyperbola.

Theorem:
In the hyperbola with the equation:
2a is the length of the horizontal axis
2b is the length of the vertical axis
2c is the distance between the foci (and length of the diagonals)
Investigation Section
Activity 1 - Two Examples...
In this hyperbola, the foci are on the x-axis, with a = 3 and b = 4. Thus the vertices of the hyperbola are (3, 0) and (-3, 0). If you are drawing this using paper and pencil, draw a rectangle centered at the origin with horizontal axis of length 2 x 3 = 6, and vertical axis of 2 x 4 = 8. The diagonals of this rectangle are the asymptotes. They have the equation:
The hyperbola has vertices at (3, 0) and (-3, 0). The hyperbola is bounded by the asymptotes, as can be seen by the graphic above.
In this hyperbola, the foci are on the y-axis, with a = 3 and b = 4. Thus the vertices of the hyperbola are (0, 3) and (0, -3). The diagonals of this rectangle are the asymptotes. They have the equation:
How can we verify these results?
First, analyze the equation for values excluded from the domain or range.
In the first hyperbola,
The second equation is almost identical to this, except we will solve for x, rather than y.