

It has now become a rather standard exercise, with available
technology, to construct graphs to consider the equation
Different values for a, b, and c will produce parabolas of different size, shape, and position. When we change c we know that the y coordinate of the vertex changes. See assignment 2: The Restless Parabola for more on this!
What happens when we change the value for b?
Let look at different values of b for the equation x^2+b+1
For b=-4,-3,-2,-1,0,1,2,3,4
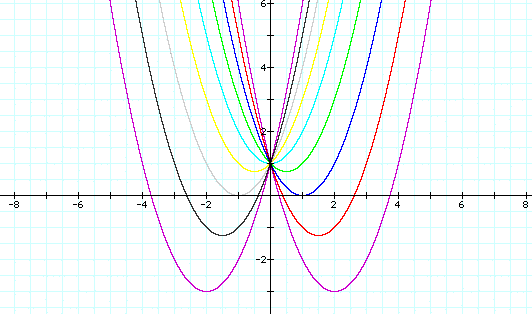
If we look very closely at the picture, it seems all the parabola meet at a central point. Might this point be the vertex of another parabola? Let's try the same graph with the line y=x+1
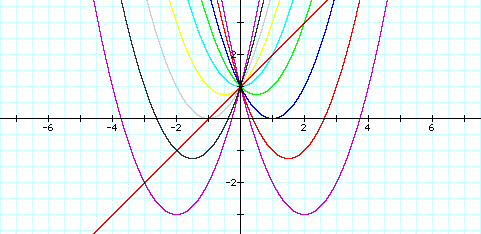
Now let's try the parabola ![]()
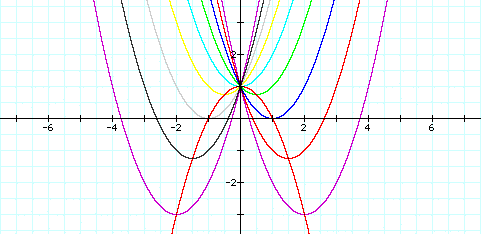
Wow! It looks like the vertexes of the parabolas are on the
parabola ![]() !
!
Can we prove this?
We know that the vertex any parabola lies on the point tangent
to the x-axis. Let's take the derivative of ![]() So, d/dx
So, d/dx![]() gives
us x=-b/2a. Plugging -b/2a for x into
gives
us x=-b/2a. Plugging -b/2a for x into ![]() ...we get
...we get ![]()
Therefore the vertex of any parabola ![]() lies
on the parabola
lies
on the parabola ![]() !
!
Now, let look for the roots of the equation with changing values of b!
Recall:
for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following picture is obtained
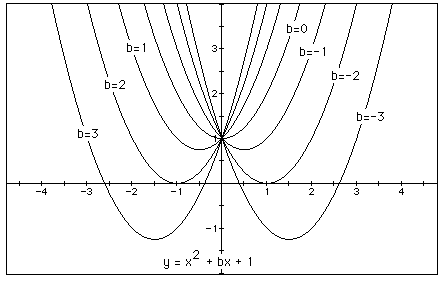
The parabola always passes through the same point on the y-axis ( the point (0,1) with this equation).
For b < -2 the parabola will intersect the x-axis in two points with positive x values (i.e. the original equation will have two real roots, both positive).
For b = -2, the parabola is tangent to the x-axis and so the original equation has one real and positive root at the point of tangency.
For -2 < b < 2, the parabola does not intersect the x-axis -- the original equation has no real roots.
Similarly for b = 2 the parabola is tangent to the x-axis (one
real negative root) and for b > 2, the parabola intersects
the x-axis twice to show two negative real roots for each b.
Let find the root(s) of the parabola by using the fact that:
the vertex of any parabola ![]() lies
on the parabola
lies
on the parabola ![]()

To find the values of the parabola that has one real root,
we solve downward parabola ![]() setting
y=0. Thus x=-1 and x=1 are the single roots for the equation for two different values of b (i.e. b=2 and b=-2).
setting
y=0. Thus x=-1 and x=1 are the single roots for the equation for two different values of b (i.e. b=2 and b=-2).
Consider again the equation
Now graph this relation in the xb plane. To do this, we graph the equation x^2+yx+1=0
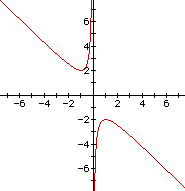
If we take any particular value of b, and overlay this equation
on the graph we add 4 line parallel to the x-axis: y=5, y=2, y=-2
and y=-5. If it intersects the curve in the xb plane the intersection
points correspond to the roots of the original equation for that
value of b. We have the following graph.
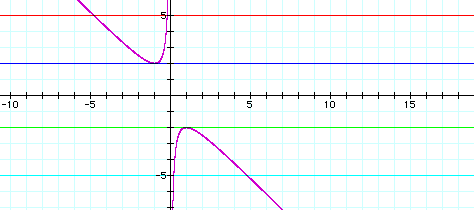
For each value of b we select, we get a horizontal line. It
is clear on a single graph that we get two negative real roots
of the original equation when b > 2, one negative real root
when b = 2, no real roots for -2 < b < 2, One positive real
root when b = -2, and two positive real roots when b < -2.
Graphs in the xc plane.
Now, let's take a look at xc plane. This means we'll just substitute
y for c in :![]()
Hey, we'll let b=2 . Now we'll graph !
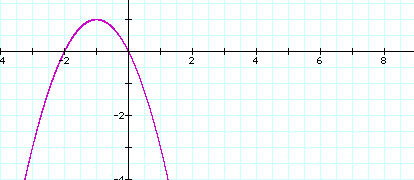
Now add lines parallel to the a-axis...
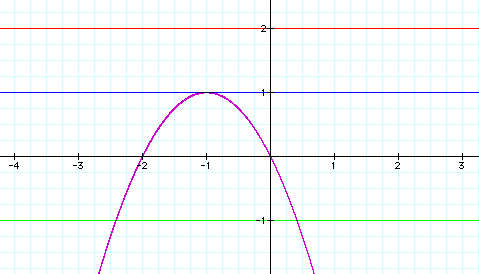
Now it's easy to see that when:
c> 1, there are no real roots
c=1, there exists one real root
c<1, there exists two real roots
See you tomorrow!!!!!!!!!