Assignment 4: The Sublime Nature of the Angle Bisector
The angle bisectors of the internal angles of a triangle are concurrent. Believe it! It's true!
Review of some definitions (for my edification!):
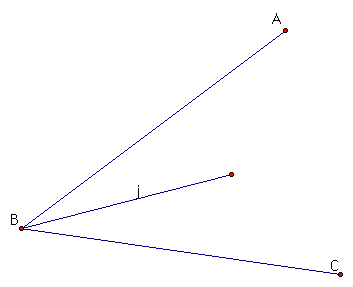
Angle bisector of a triangle is a line segment that bisects one of the vertex angles of a triangle. An angle bisector is equidistant from the sides of the angle when measured along a segment perpendicular to the side of the angle.
Here line j is is an angle bisector of B

Line DE is perpendicular to line AB and line EF is perpendicular to BC
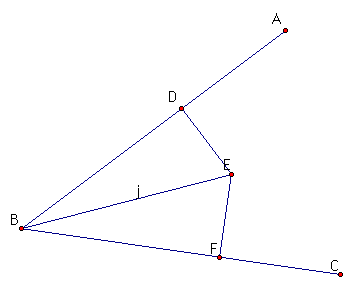
By definition of angle bisector we know DE is congruent to EF!
Another term we need to know:
Two or more lines are said to be concurrent if they all pass through a common point.
Let us Begin...
Draw triangle ABC

Construct an angle bisector of A and construct an angle bisector of B. Where these two bisectors intersect is the point D
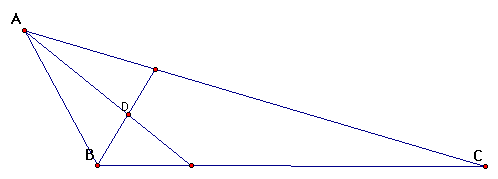
Draw a line segment CD.
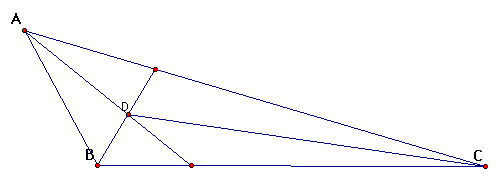
Remember we are trying to prove that three angle bisectors are concurrent (i.e. they all pass through a common point) We've got 2 angle bisectors...so, all we need to do is show that CD is an angle bisector of C. Remember, an angle bisector is equidistant from the sides of the angle when measured along a segment perpendicular to the side of the angle. We'll draw a perpendicular line from the intersection D to the line AC. Likewise, we need a perpendicular line from D to the line BC and a perpendicular line from D to line AB.
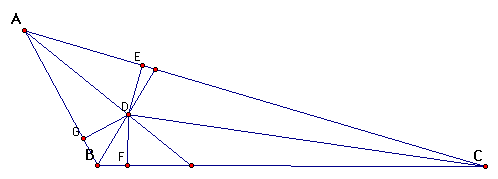
DG perpendicular to AB and DE is perpendicular to AC. By definition
of the angle bisector, DG is congruent to DE. Likewise, DG is
congruent to DF and DF is congruent to DE.
DE and DF are the distances from D to the sides of angle C.
We know that DF is congruent to DE; thus, CD is the
angle bisector of C.
CD, AD, and BD are angle bisectors. The angle bisectors intersect
at point D. Therefore, the angle bisectors of the interior angles
of a triangle are concurrent.
The proof is in the pudding! The End.