Assignment 8: Altitudes and Orthocenters

Large Print Edition!

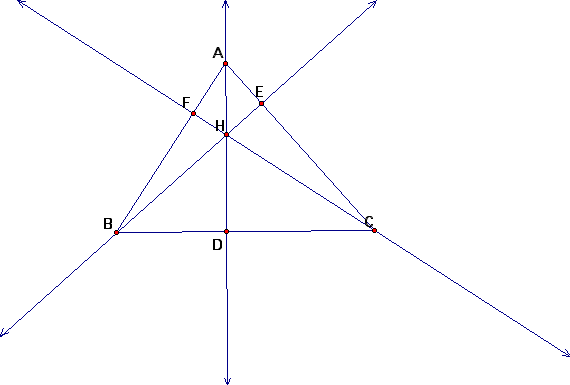
Given triangle ABC. Construct the Orthocenter H. Let points D, E, and F be the feet of the perpendiculars from A, B, and C
respectfully. Prove:

PART 1:

PART 2:

Our Triangle!

Area of triangle AHB = 1/2 x HF x AB=T(1)

Area of triangle BHC = 1/2 x HD x BC=T(2)

Area of triangle AHC = 1/2 x HE x AC=T(3)

Area of triangle ABC = area AHB + area BHC + area AHC

Area of triangle ABC = T

Using our notation T; gives us the following...

Clearly the area of ABC divided by itself is 1

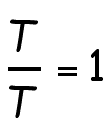
With a little substitution we have:

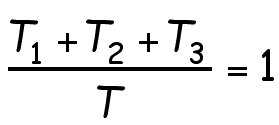
And with a little more substitution this equals:

And with some cancellations we have:

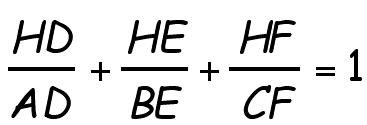
This proves PART 1

Now we will prove PART 2:

From the picture of our triangle it is easy to see that:

So, we have proved PART 2!

But what if triangle ABC is obtuse?

The Orthocenter lies outside the triangle PART 1 and PART 2 (i.e. the equations we just proved) do not hold.

Let look at Orthocenter K which lies outside triangle ABC.

If we look closely we can see that C is an orthocenter for triangle AKC

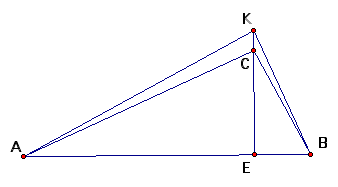
Homework: Prove PART 1 and PART 2 for the triangle AKB

Good Luck!