Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.

We can think three cases in the situation above(given circles have red colors) and in each case we can get two kinds(pink color and blue color) of tangent circle like the following.(Of couse, there are tangency cases between each cases)

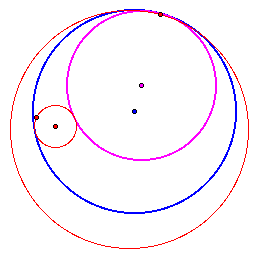
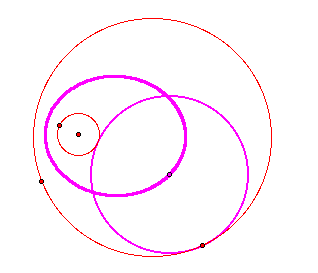
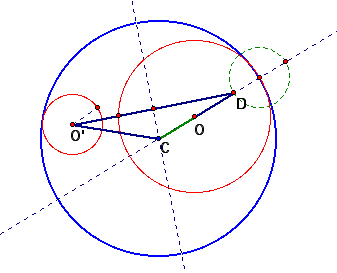
Method 1 When the smaller circle is external to the tangent circle.

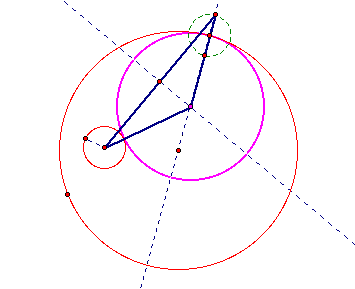
(1) Draw the line passing through a center of the bigger circle

(2) Draw a circle with radius of the smaller circle at an intersection getting from (1)

(3) we can get the isosceles triangle above using the property of perpendicular bisector

(4) Our pink circle becomes tangent to two red circles

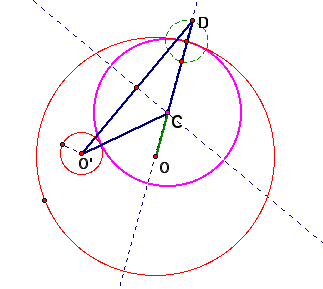
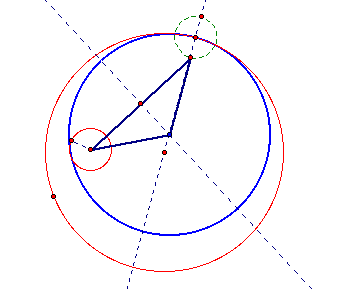
(1) Draw the line passing through a center of the bigger circle

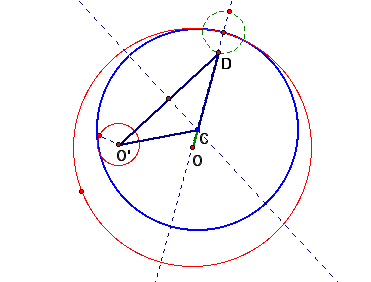
(2) Draw a circle with radius of the smaller circle at an intersection getting from (1)

(3) we can get the isosceles triangle above using the property of perpendicular bisector

(4) Our blue circle becomes tangent to two red circles

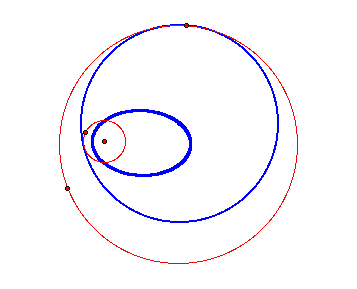
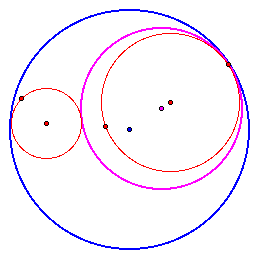
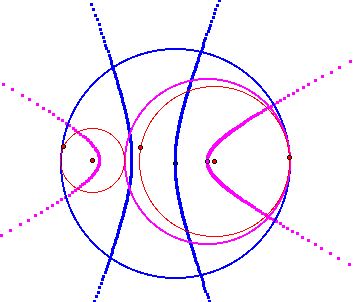
Method 2 When one circle intersects with another circle in two different point

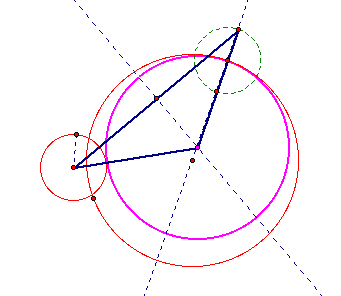
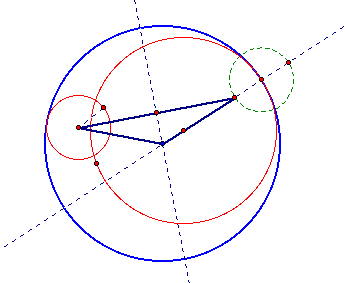
We can get the isosceles triangle above as moving of the smalller circle from the method1 using the funtion of GSP.

Our pink and blue circle becomes tangent to two red circles

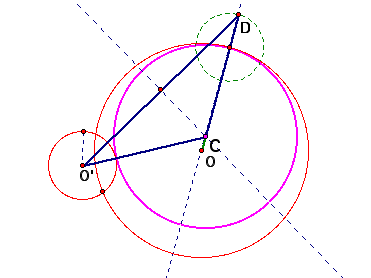
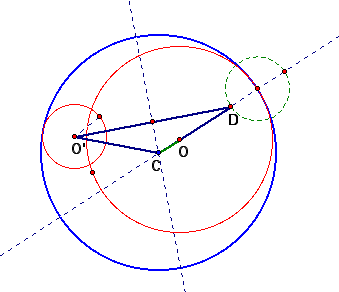
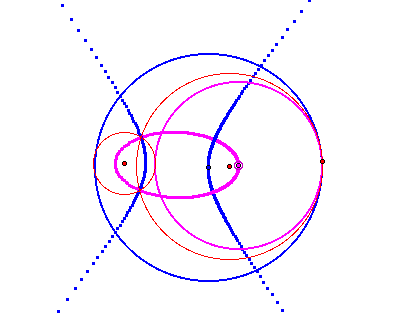
Method 3 When one circle lies outside of another circle

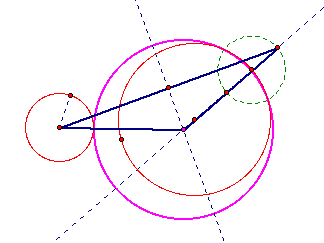
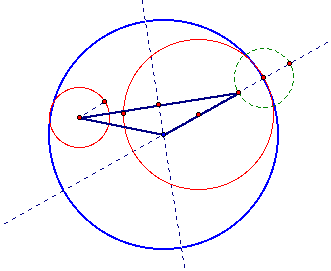
We can get the isosceles triangle above as moving of the smalller circle from the method1 using the funtion of GSP.

Our pink and blue circle becomes tangent to two red circles

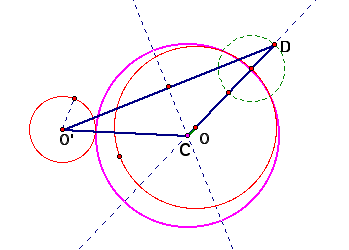
Return to Hyungsook's homepage