Assignment # 1

The purpose of this assignment is to find two linear functions f(x) and g(x) such that their product h(x) is tangential to each function at two distinct points. Therefore

f(x) * g(x) = h(x).

Let’s begin by examining quadratic functions, since the product of two linear functions will always be quadratic. The general form is

ax² + bx + c.

Let’s examine the graph of different quadratic functions beginning with the basic function y = x². We obtain the following graph for the corresponding quadratic functions.

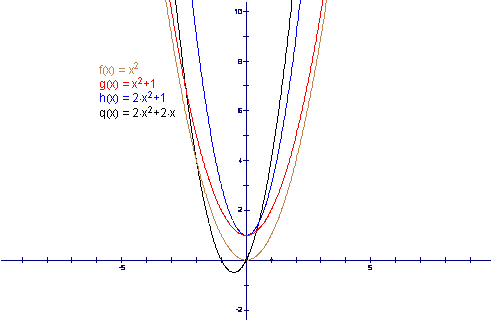
We see that all the graphs of quadratic functions are parabolas. Parabolas are always symmetrical to the y-axis or a line parallel to the y-axis. Since a parabola is a symmetrical function dealing with two linear functions that are reflections of each other would allow for the linear functions to be tangential at two distinct but mirror points. In order for linear functions to be reflections of each other their slopes must be of equal magnitude but in opposite direction.

We now have a good staring point and can begin with two linear functions that are reflections such as

g(x) = x² +1

f(x) = -x² +1.

We can examine where these three functions intersect by graphing these functions and their product and obtaining the following graph:

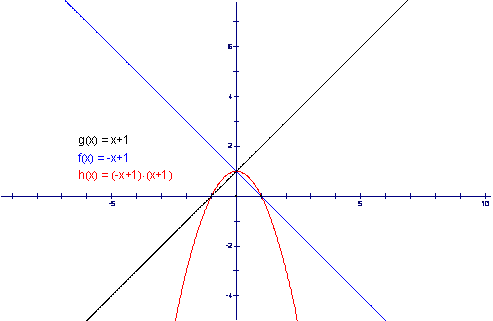
We can see these functions are not tangential to their product. In fact each function intersects the product at two distinct points. We can adjust g(x) and f(x) by increasing the slope and examine the effect on h(x). Now we obtain the following graph for the same equations with slopes of 2 and -2.

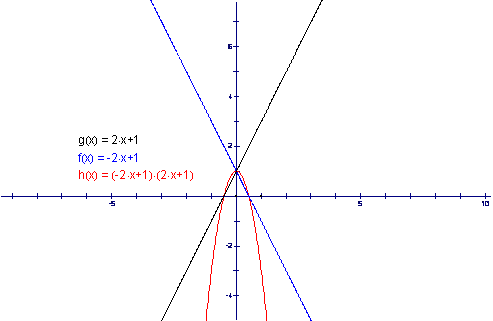
We can see that intersections are the same only the steepness of the graph does. Therefore changing the slope doesn’t seem productive. We can now focus on the y-intercept. If we change the intercept for one function and keep the other the same we obtain:

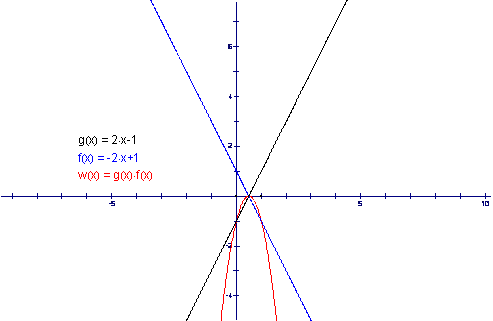
This is not any closer to what we are looking for. We can see different signs on the y-intercept only moved the entire graph. Now we need to examine the effect of the difference between the y-intercepts on the functions.

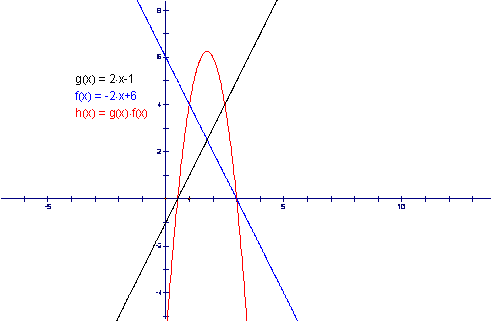
It seems as the difference increases the parabola seems to “move up.” It seems we have increased the difference between the intercepts too much and the parabola is now higher up. If we adjust and have a smaller difference between the intercepts we obtain the following graph.

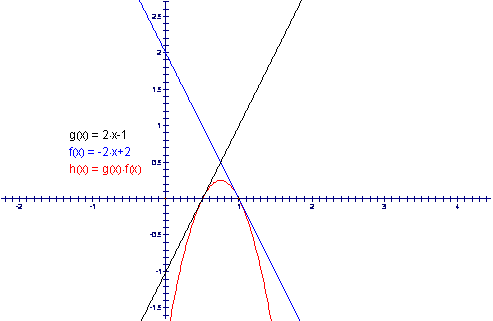
This graph seems to be a solution. We can take a closer look at this graph to see if it does in fact produce a solution.

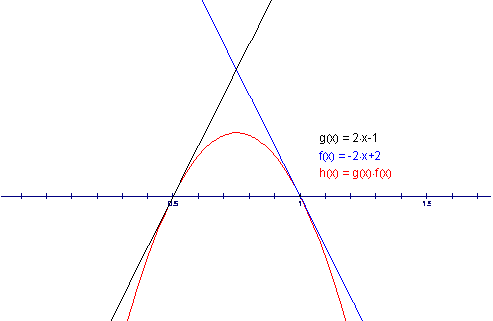
It seems from the graph that we have obtained two linear functions that are tangential to their product. We can check to see if this is true by taking the derivative of h(x). If h’(x) is equal to the slope of the linear functions at the corresponding x values then we have found the right functions. Since

h(x) = -4x² +6x -2

then,

h’(x) = -8x +6

We can now substitute into the equations the values of x from the graph.

For x = 0.5 and x = 1.0 we obtain the following equations:

h(1.0)= -8(1) + 6 = -2

h(0.5) = -8(.5) +6 = 2.

Since these values coincide with the slopes of the corresponding linear functions then we know they are in fact tangential at these x values. Therefore our functions are

f(x) = -2x + 2

g(x) = 2x – 1.

We can check to see if this pattern holds true for any two linear functions whose slopes are equal but opposite and the difference of the y-intercepts is 3. We obtain the following graph for such functions.

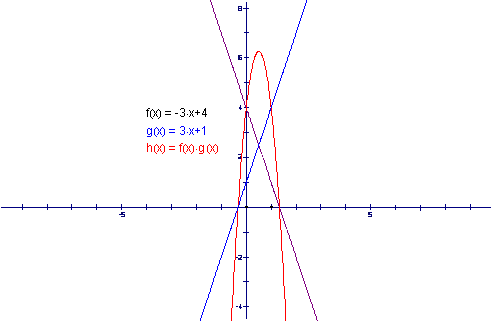
We can see these functions do not work. We can check to see if we need to focus on the absolute value of the difference of the y-intercepts. Using this new approach we obtain the following graph.

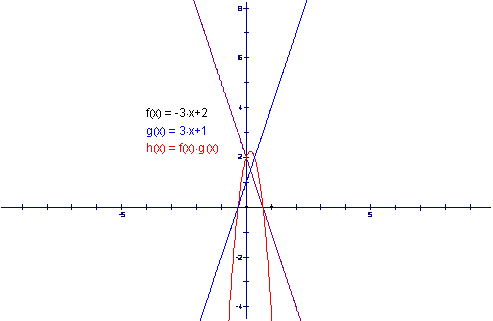
Again this does not work. Since the functions that did give a solution had y-intercepts of opposite signs then we should try changing one of the signs of the y-intercept and see if the functions work.

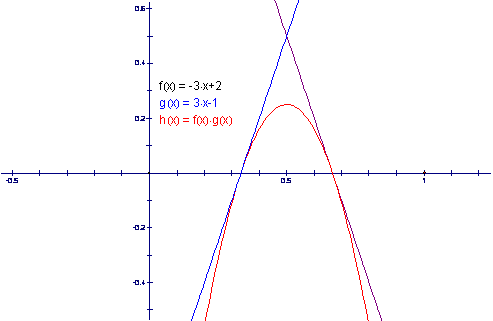
We can see that this works. Therefore we now can hypothesis that any two functions with :

· equal but opposite slopes,

· y-intercepts where the absolute value of their difference is 1 and

· y-intercepts with opposite signs

will give a solution to this problem. We can try a few different functions to further test our hypothesis.

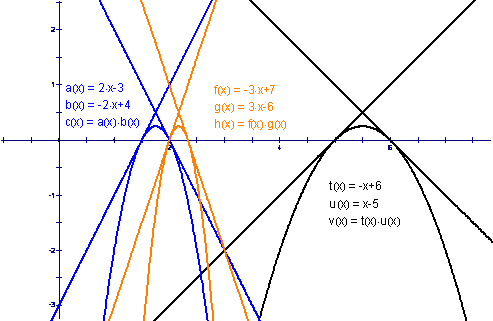
We can see by inspection that our hypothesis holds true for any two functions with these properties. Therefore all functions of the following form will be a solution to this problem.

mx + b and –mx + |b| ± 1