Exploration in Polar Equations
Hello sports fans! And
welcome to another episode of "Math stuff you never never
knew anything about". Today we will be exploring the exciting
and interesting world of polar equations. (Try to contain your
excitement.)
But seriously, what
we have here is another exploration where I try to make sense
of a new type of equation. I'll be looking for the relationship
between the given variables and the graph they produce. If you
liked me in "Explorations with tangent circles", or
"Parametric Equations and Linear Functions", you are
sure to enjoy this as well.
Today we will be looking
at equations in the form of 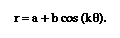 This
is known as a polar equation. Polar equations can be recognized
as they express r as a function of theta
This
is known as a polar equation. Polar equations can be recognized
as they express r as a function of theta  Lets
begin our exploration by choosing values of a, b and k, such that
a and b are both equal to 3, and k is 4. The graph of this equation
is:
Lets
begin our exploration by choosing values of a, b and k, such that
a and b are both equal to 3, and k is 4. The graph of this equation
is:
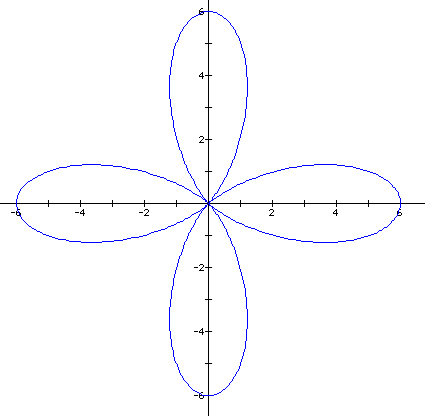
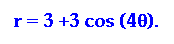
As you can see, this
is the traditional rose graph many of us saw in high school algebra
II/ trig. In the case above, our rose has 4 leafs which reach
a maximum of r = 6 . Our first glance at conjecture might be that
k represents the number of leaf for given graph. Let's change
the k in our equation to 5, and see if we get five leafs.
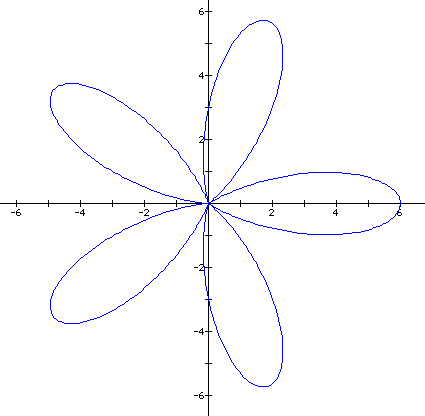
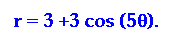
What do you know, it
looks like our conjecture holds. Let us now look at varying a
and b and see what they do to the graph.
Our next equation will
be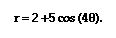 We believe that based on our conjecture
that the graph will have four leafs. Let's see...
We believe that based on our conjecture
that the graph will have four leafs. Let's see...
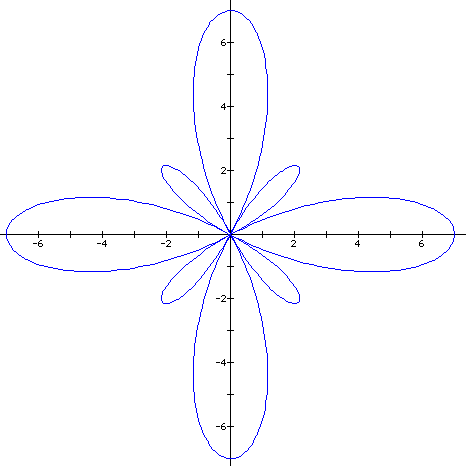
Uh oh! We don't have
four leaves, we actually have 8! The larger leaves have a maximum
of r = 7, the shorter leaves have a maximum of what appears to
be r = 3. We need to rethink our hypothesis. Why would we have
more leaves when the values for a and b are not equal? It would
seem that a and b have something to do with the leaves. Let's
go back to our earlier equations and graphs.
When k was 4, and a
and b were both 3, we know that we had four leaves that reached
a maximum of r = 6. when k was five and a and b were both three,
we had five leaves that had a maximum of r = 6. If we add the
values for a and b we get six as well. Perhaps this is a relationship
we can test out with our latest graph.
When k was 4, and a
= 2 and b = 5, we got eight leaves, four of which had a maximum
of r = 7. Seven is the sum of a and b, so our hypothesis holds.
But it doesn't explain why did we also get four leaves whose maximum
was 3. Aha! - the difference of b and a is three. Perhaps that
is where the other leaves come from. Looking back it makes sense,
that if a an b are the same, that their difference would be zero.
That would explain why the other leaves were not there.
Okay, so our newest
conjecture for the form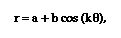 is that a+b will
represent the length of k leaves of the rose, and b - a will represent
k leaves of the rose. Let's look at another equation and make
some predictions.
is that a+b will
represent the length of k leaves of the rose, and b - a will represent
k leaves of the rose. Let's look at another equation and make
some predictions.
For our next example,
let's take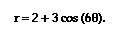 According to our conjecture, our
graph should have six leaves of maximum length 5, and six leaves
of maximum length 1. Survey says...
According to our conjecture, our
graph should have six leaves of maximum length 5, and six leaves
of maximum length 1. Survey says...
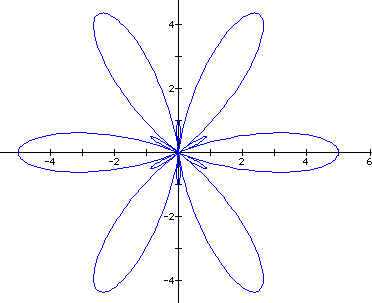
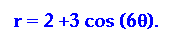
We are correct!
There is one thing that
bothers me, what would happen if a was greater than b. This would
mean that the difference would be negative. How could we have
negative maximums? Let's look at what might happen when we graph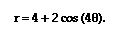
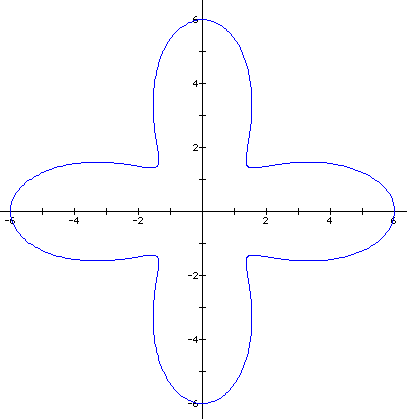
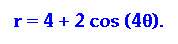
This is not good. It
appears that we have four leaves with a maximum of r = 6, but
these leaves are not closed like the other graphs. They do not
go through the origin as the others do. Instead, they have a minimum
value of r = 2. Two is the difference of a - b in our equation,
so the minimum values makes logical sense. If we look at another
equation, we should now be able to predict its shape completely.
How about the equation
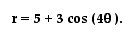 Our graph should have five leaves
that have a maximum vale of r = 8, and should have minimum values
of r = 2. Let's see what happens...
Our graph should have five leaves
that have a maximum vale of r = 8, and should have minimum values
of r = 2. Let's see what happens...
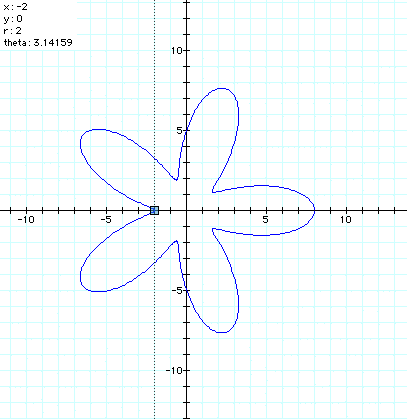
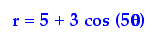
One again, we
are correct!
In summary, we now can
predict the graph of any polar equation in the form of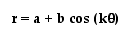 .
.
- If b is greater than
a, we
will have k leaves with a maximum r value of a + b, and a minimum
of zero. As well as k leaves with a maxim value of r = b - a
, and a minimum value of zero.
- If b is less than a, we will get k leaves
with a maximum r value of a +b, and a minimum r value of a -
b.





