Assignment 2:
Explorations in Graphs of Quadratic
Equations
In this assignment, we were involved in exploring
the graphs of the general quadratic equation
and studying the effects of the variables
a, b and c on the graphs of these equations. In teaching this
material, many teachers are aware of how each variable can affect
the shape and position of the graph. The important thing in my
opinion is to get your students to discover these patterns and
be able to use them when solving quadratics by graphing, or as
a continuing effort to understand a transformational approach
to graphing functions.
We know that for any equation in the form
of 
, where a, b and c are any real numbers
and a is not 0, the graph will be a parabola. What we would like
to know is how the variables a, b, and c affect the shape and
orientation of the graph.
Let's begin with the general equation 
. In this case, a
= 1 and b = c = 0
Notice that the parabola shows symmetry to
the y axis, and that its vertex is located at the origin. If we
were to change the value of a, what types of changes would we
find?
Here are graphs where a = 2, a = 3, a = -2, a = -4, and a = 1/2
Looking at these graphs we can make some basic
observations.
It appears that increasing the value of a
makes the parabola more narrow, as if it had been compressed horizontally.
When a is decreased, it appears to stretch the parabola horizontally.
The y coordinates of our original equation have been multiplied
by a given scale factor of a. This either causes the y values
to increase more sharply, causing the shape to narrow, or for
them to increase at a smaller rate, causing the widening of the
parabola.
The observation holds true as long as a is
positive. When a is negative, the parabola opens pointing down.
Let's look a bit more closely at this to see what is truly happening.
On the graph below we have the equations 
and 
. Notice
how similar they appear. In fact, the graph when a = -1, appears to be the same as when a = 1, except
that it has been reflected across the x axis.
It appears that this is the function of the
negative sign in relation to the value of a. Let's check our theory
by plotting several equations whose a values are opposites.
graphs
graphs
graphs
graphs
Notice that in each case, the parabolas are
exactly the same except for their reflection across the x axis.
The only possibility left for a is a = 0.
When we defined the general equation of a parabola, we stated
that a could not equal 0. Why is this? Well, if a were zero, then
when we multiplied it by the quadratic term, it would also become
zero. Without a quadratic term, you can't have a quadratic equation.
We would be left with the linear equation y = bx +c.
How does the value of c effect the location
and shape of the graph? Let's look into it...
Let's begin again with the simple equation
. When we graph it, we see this:
Where is the graph 
in relation to the original? It appears to look the same, except
that it has been moved up two units.
What if we graphed 
? We might think that it will be the
same as our original, except moved one space down. Let's see...
It would seem that the value
of c moves the vertex of the parabola along the y axis. Moving
it up c spaces when c > 0, and down c spaces when c < 0.
Let's see what happens when we make our equation a bit more complex.
Based on our hypothesis, the
vertex of the parabola should be at 2 on the y axis,. Let's see...
Well, it appears that our idea is false. The
vertex is not located at 2 on the y axis. It appears to
be located at (-2, -2). However, the parabola does intersect the
y axis at -2. Maybe this has to do with the value of c. Let's
find out.
We now think that when a parabola is in the
form of , that c represents the y intercept
of the parabola. Lets explore this with a few equations.
graph
graph
graph
Based on our new idea, each of these graphs
should intersect the y axis at 2. Do they?
Yes they do! It appears we are back on the
right track. However, we still don't know one crucial thing about
our parabolas, where the vertex will be located. In order to determine
the location of our vertex in relationship to ,
we will need to investigate how b effects our graph.
Let's take a look at several quadratics and
their vertices, and see if we can find a relationship between
b and the location of the vertex.
vertex (1, 4)
vertex (2, 1)
vertex (-2.5, -1.25)
vertex (-1.5, 2.75)
One pattern appears to have something to do
with the x value for the vertex and the value of b. In these cases,
each appears to be equal to -1/2 b. The y values are related to
this as each y value is the difference of c and the square of
the x coordinate value.
Let's make a guess and test our hypotheses...
To find the x coordinate of the vertex we
should take -1/2(b) or -1/2(-6) = 3.
The y coordinate should be 6 - 9 = -3.
so the vertex of should
be (3, -3). Let's graph it and see.
It is! We should try our theory when a does
not equal 1.
Based on our formulas, the vertex for this
parabola should be at (-2,
-5). Since x = -1/2(4) = -2, and y = -1
- 4 = -5.
However, it is not where we thought it would
be. Since y is dependent upon x, lets see what happened to x first.
We thought the x coordinate would be -2 and it is -1. Would we
have been correct if a had been 1 in our original equation? Let's
find out.
Our guess was correct for a = 1, but for a
= 2, our coordinate was half as large as we thought. Perhaps there
is a relationship between a and b and the x coordinate. Let's
look at some equations whose b and c remain constant, and vary
the a to see how it effects the vertex of the parabola.
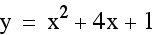vertex (-2,
-3)
vertex (-1,
-1)
vertex
(-2/3, -5/9)
vertex (-1/2, 0)
As you can see another pattern begins to emerge.
Each new vertex has an x coordinate that is equal to the vertex
where a=1, divided by the new coefficient of a. This means, our
rule for locating the x coordinate of the vertex is actually x
= -1/2b(1/a) or x = -b/2a. If we were to graph each of these equations
for the x coordinate, what would we find?
These lines are known as the line of symmetry
for a given parabola. They will always have the equation x = the
x coordinate of the vertex.
The above excursions can allow a teacher to
get their students to think about the relationships that exist
within a quadratic equation. Instead of simply telling or demonstrating,
these ideas could and should be posed as problems to your students,
allowing them to find patterns and connections. These patterns
can also be revisited after teaching completing the square. Have
students use completing the square to write the equation in the
form of y = (x-h)^2 + k. These efforts will lead to deeper understanding
of concepts and get your students thinking about math, not just
doing it.
RETURN TO Andy's Page