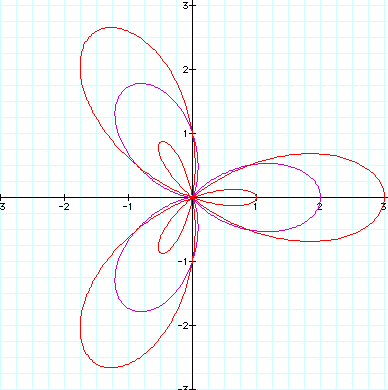
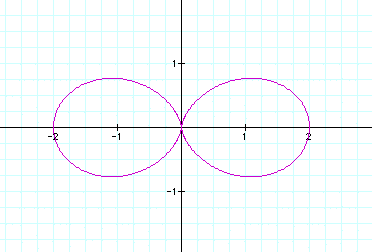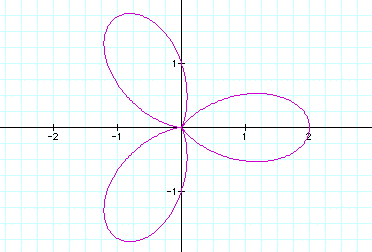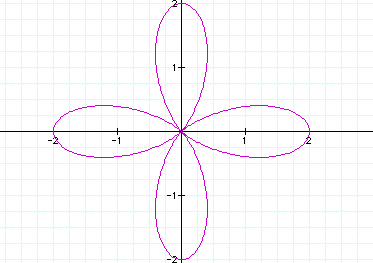1. When a and b are equal, and k is an integer, this is a textbook version of the "n-leaf rose"
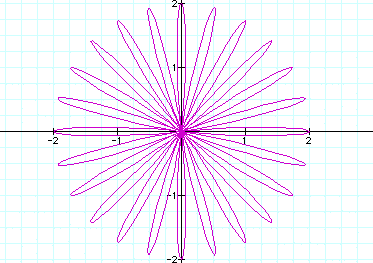
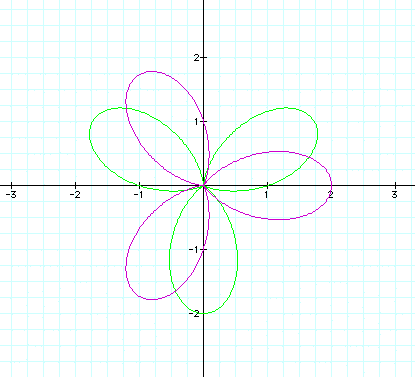
Let a = 1, b = 1 and k = 2 Let a = 1 , b=1 and k = 3 Let a =1, b = 1 and k = 4 Notice that for k=2 there are two leaves, for k=3 there are 3 leaves and for k=4 there are four leaves. Lets see what would happen if we let k = 24.
Sure enough we got 24 leaves :)
2. If a < b and k is an integer.
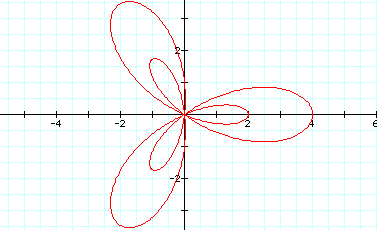
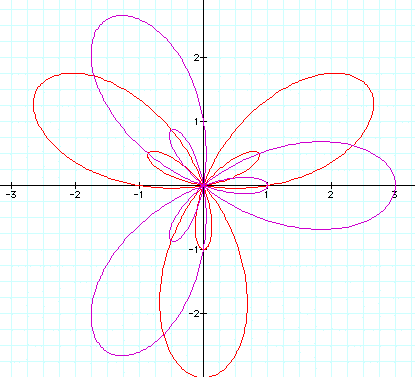
Let a = 1, b = 2 and k = 3 The purple rose is the first case we looked at the the red rose is the current case. When we changed b from 1 to 2 we now have an inter "n-leaf rose"
Lets look at what happens as b increases
As b increases the inter rose is getting larger by 1. If b = 1 then the inter rose was at 0 on the x-axis, if b=2 then the inter rose was at 1, if b= 3 then the inter rose is at 2 and so on.
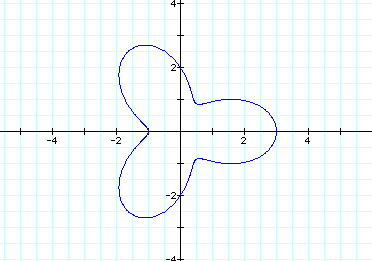
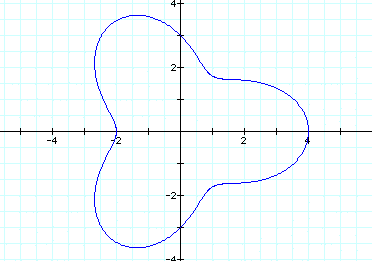
3. If a > b and k = integer.
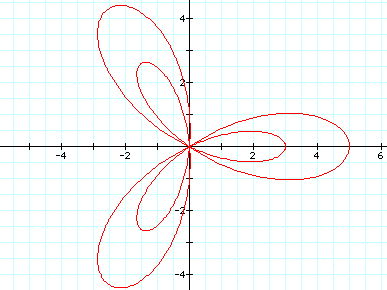
Let a = 2, b=1 and k=3 Now that a is larger than b we still have three leaves; however, it does not meet at the origin anymore. Lets look at if a gets larger and b stays the same.
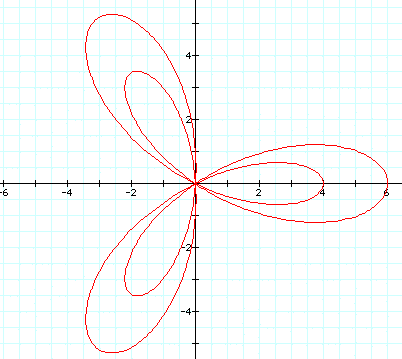
Let a =3, b = 1 and k = 3 Now that a is a little larger than b it looks as if the rose is getting further away from the origin. Lets make a even larger. Isn't this exciting:)
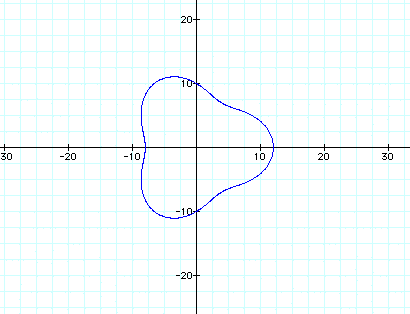
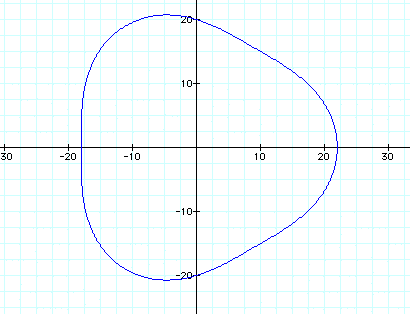
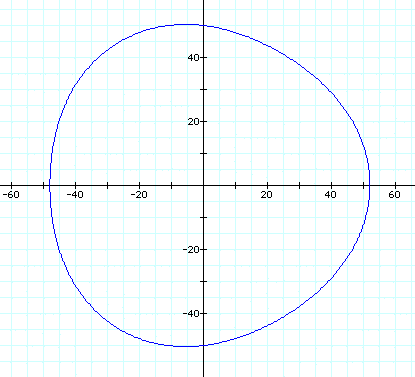
Let a = 10, b = 2 and k = 3 Let a = 20, b = 2 and k = 3 Let a = 50, b = 2 and k = 3 The further away a and b are from each other the further away the rose is from the origin.
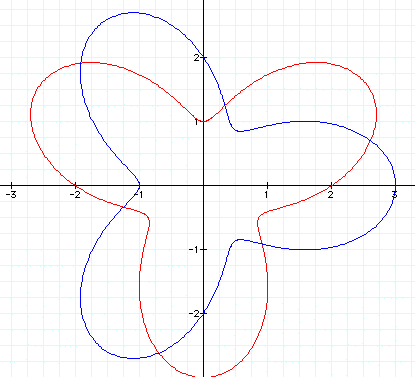
4. Lets now replace cos with sin, lets take a look at an example from each of the previous cases. I have included the cos graph with the sin graph to make the comparsion easier.
RETURN TO JENNIFER WEAVER'S HOME PAGE