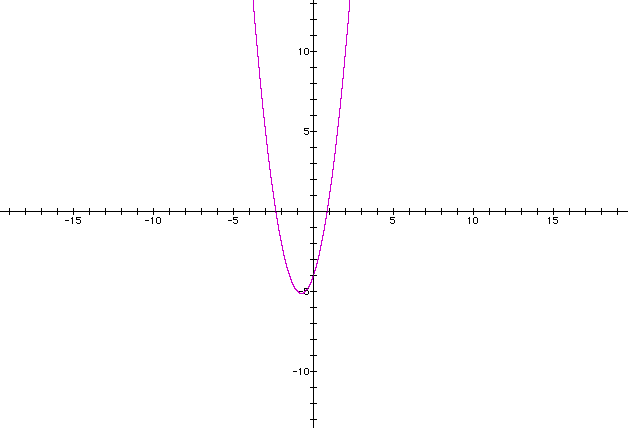Graph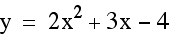

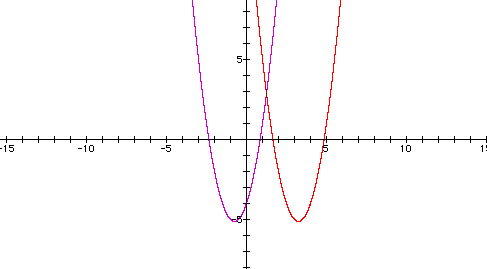
i. Overlay a new graph replacing each x by (x-4).

ii. Change the equation to move the graph into the second quadrant.

iii. Change the equation to produce a graph concave down that shared the same vertex.

 

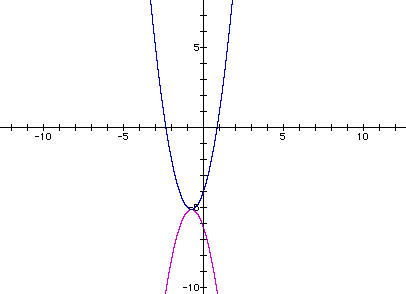
First let's take a look at what the graph of this quadratic looks like.

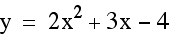
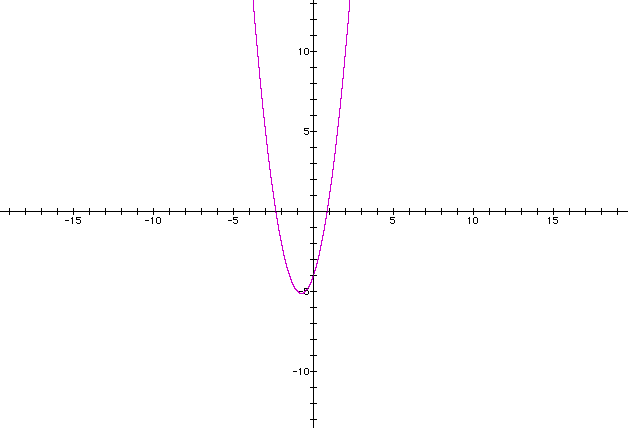
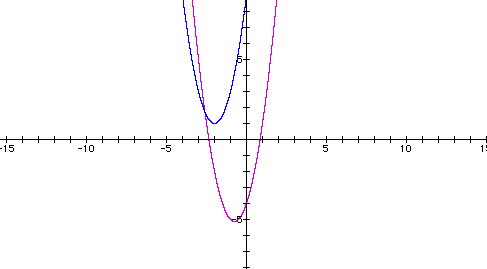
I found the same quadratic equation by completing the sqaure. For an explaination on how to complete the square click here.

y = 2(x + (3/4) )^2 - (41/8)

This quadratic equation is in the quadratic form

y = a (bx - h )^2 +k, we can compare different quadratic graphs by looking at the parent graph of y = x^2

If the absolute value of a is greater than 1 then your graph will stretch vertically by a.

If the absolute value of a is less than 1 then your graph will compress vertically by a.

If the absolute value of b is greater than 1 then your graph will compress horizontally by 1/b

If the absolute value of b is less than 1 then your graph will stretch horizontally by 1/b

The vertex of the the graph is (h,k)

If h is negative then the graph will move to the right, h units

If h is positive then the graph will move to the left, h units

If k is positive then the graph will move up, k units

If k is negative then the graph will move down, k units

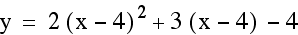
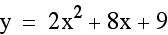
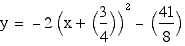
Return to :Jennifer Weaver's Home Page