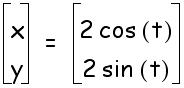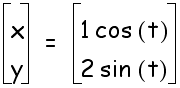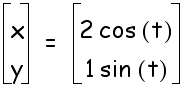ASSIGNMENT
#10
PARAMETRIC
CURVES
A
parametric curve in the plane is a pair of functions:
x = f(t)
y
= g (t)
where
the two continuous funtions define ordered pairs (x,y). The two
equations are usually called the parametric equations of a curve.
The extent of the curve will help depend on the range of t.
In many applications, we think of x and y "varying with
time t" or the angle of rotation that some line makes from
an initial location.
We
will investigate
x
= a cos (t)
y
= b sin (t)
for
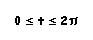 Let's
look at a couple different cases;
1.
a=b
Let
a = b =2
If
you solve the first equation for cos t and the second equation
for sin t.
cos
t = x/2 and sin t = y/2
Now
use your trig identity cos^2 t + sin ^2 t =1 to rewrite the equation
to eliminate t.
cos
^2 t + sin ^2 t = 1
(x/2)^2
+ (y/2)^2 =1 (by subsitution)
x^2/4
+y^2/4 =1
x^2
+ y^2 = 4 (Multiply each side by 4)
As
you can see by looking at the equation or the graph this is a
circle with center at (0,0) and a radius of 2. As t increases
from
Let's
look at a couple different cases;
1.
a=b
Let
a = b =2
If
you solve the first equation for cos t and the second equation
for sin t.
cos
t = x/2 and sin t = y/2
Now
use your trig identity cos^2 t + sin ^2 t =1 to rewrite the equation
to eliminate t.
cos
^2 t + sin ^2 t = 1
(x/2)^2
+ (y/2)^2 =1 (by subsitution)
x^2/4
+y^2/4 =1
x^2
+ y^2 = 4 (Multiply each side by 4)
As
you can see by looking at the equation or the graph this is a
circle with center at (0,0) and a radius of 2. As t increases
from 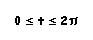
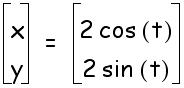
 2.
a < b
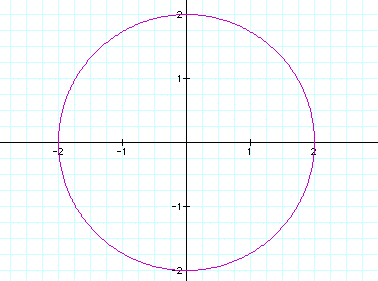
Let
a =1 and b =2
2.
a < b
Let
a =1 and b =2
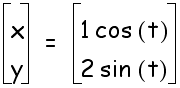
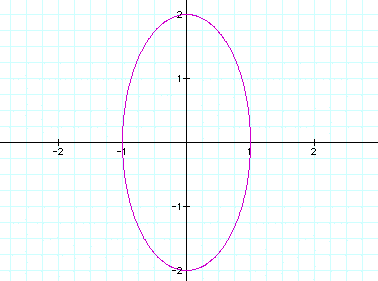 Notice
that b is larger than a, since sin is connected with the y- coornidate,
the graph did exactly what should be expected it should strech
vertically. Now can you determine what will happen if we make
b smaller than a?
3.
a > b
Let
a =2 and b =1
Notice
that b is larger than a, since sin is connected with the y- coornidate,
the graph did exactly what should be expected it should strech
vertically. Now can you determine what will happen if we make
b smaller than a?
3.
a > b
Let
a =2 and b =1
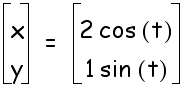
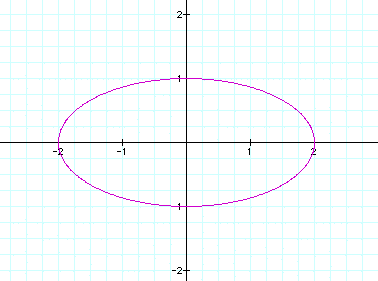 You
probably guessed it. That's right since the x-coorndinate is connected
to cosine then the circle should strech horizontally.
RETURN
TO JENNIFER WEAVER'S HOME PAGE
You
probably guessed it. That's right since the x-coorndinate is connected
to cosine then the circle should strech horizontally.
RETURN
TO JENNIFER WEAVER'S HOME PAGE