Explorations with Linear Functions

by: Lauren Wright

In this exercise, I explored the behavior of linear functions.

I made up four linear functions and then looked at the behavior of the graphs when pairs of the functions were: 1) added, 2) multiplied, 3) divided, and 4) composed.

The four linear functions I worked with were:

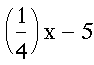
First, I paired and . Observe the graph.

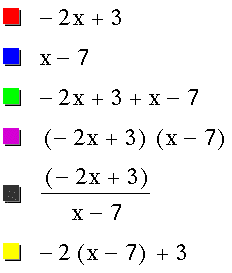
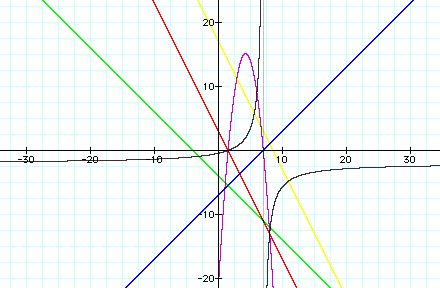
Second, I paired 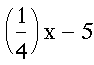and . Observe the graph.

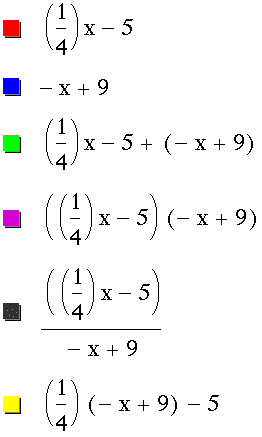
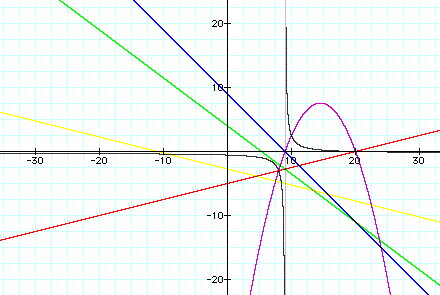
Third, I paired and 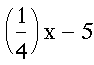. Observe the graph.

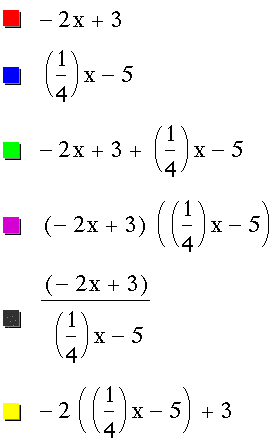
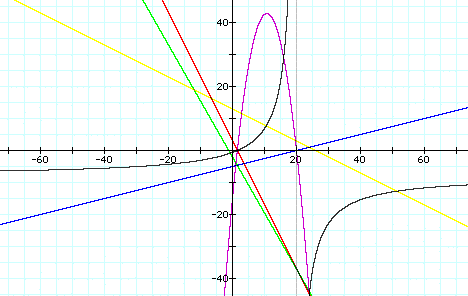
What conclusions can we draw after looking at these graphical representations?

1. The sum of two linear functions forms a new linear function.

2. The product of two linear functions forms a new quadratic function.

3. The quotient of two linear functions forms a new hyperbolic function.

4. The composition of two linear functions forms a new linear function.

After I explored some specific cases, I wanted to look at some general ones...

Linear functions are generally of the form y = mx +b.

So, I looked at f(x) = ax + b and g(x) = cx + d, where a, b, c, and d are arbitrary constants.

Sum

From the graphs, I know that this should be a linear function.

With some algebraic manipulations, I can make it look like a linear function:

(rewrite in a different order using commutativity)

(factoring x out of the first two terms)

Thus, we have a linear function - keeping in mind that since a, b, c, and d are arbitrary, their sums/differences/products/quotients are as well.

Thus, we have a linear function.

Product

Recall first that quadratic equations are of the form:

From the graphs, I know that this should be a quadratic function.

Again, with some algebraic manipulations, I can make it look like a quadratic function.

(using FOIL)

(factoring x out of the two middle terms)

Thus, we have a quadratic function.

Quotient

Recall first that hyperbolic equations are of the form:

where (h, k) is the center of the hyperbola.

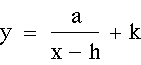
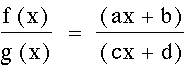
From the graphs, I know that this should be a hyperbolic function.

Once again, with some algebraic manipulations, I can make it look like a hyperbolic function.

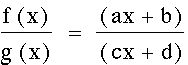
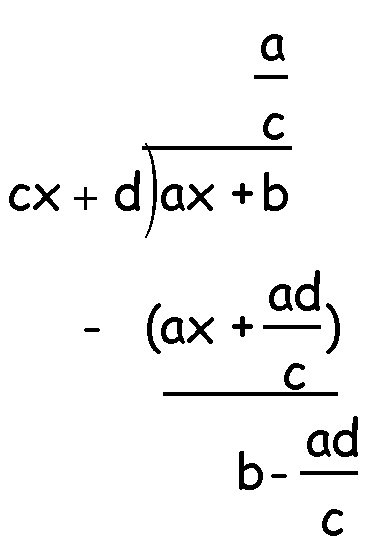(using long division)

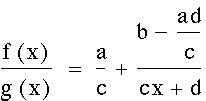
Thus, we have a hyperbolic function - keeping in mind that since a, b, c, and d are arbitrary, their sums/differences/products/quotients are as well.

Composition

From the graphs, I know that this should be a linear function.

Lastly, some simple algebraic manipulations to make it look like a linear function.

(using distributive property)

Thus, we have a linear function.