Exploring Parametric Equations
of the form:
 ,
,  ,
,  , etc.
, etc.

By: Lauren Wright
Let's first look at what happens when
a = b for  .
.

 We see that parametric equations of
this form with a = b will form circles with radius =
We see that parametric equations of
this form with a = b will form circles with radius =  .
.
Now let's look at what happens when
a < b for  .
.

 We see that parametric equations of
this form with a < b will form ellipses with the major axis
equal to the greater of
We see that parametric equations of
this form with a < b will form ellipses with the major axis
equal to the greater of or
or and
the minor axis equal to the smaller.
Again, when
and
the minor axis equal to the smaller.
Again, when  ,
we have a circle.
,
we have a circle.
Now let's look at what happens when
a > b for  .
.

 As we can see, the same is true for
a < b and a > b.
As we can see, the same is true for
a < b and a > b.
Let's look now at equations of the
form  for a = b.
for a = b.

 We see that parametric equations of
this form with a = b will form segments with a slope of -1 and
y-intercept = x-intercept = a = b.
We see that parametric equations of
this form with a = b will form segments with a slope of -1 and
y-intercept = x-intercept = a = b.
Now let's look at what happens for
a < b with  .
.

 Here we see that parametric equations
of this form with a < b will form segments with slope =
Here we see that parametric equations
of this form with a < b will form segments with slope =  , y-intercept = b, and x-intercept = a.
, y-intercept = b, and x-intercept = a.
Lastly, let's look at what happens
for a > b with  .
.

 Once again for the parametric equation
of the form
Once again for the parametric equation
of the form  , the graphs when a < b have
the same characteristics of the graphs when a > b.
, the graphs when a < b have
the same characteristics of the graphs when a > b.
Now, let's take a look at  for a = b.
for a = b.

 This gives us a diamond-like shape
with x-intercept = y-intercept = +a = +b.
This gives us a diamond-like shape
with x-intercept = y-intercept = +a = +b.
Next, let's look at  for a < b.
for a < b.

 This time, we get more diamond-like
shapes, but they are not all similar. When a < b, x-intercept
= +a and y-intercept = +b.
This time, we get more diamond-like
shapes, but they are not all similar. When a < b, x-intercept
= +a and y-intercept = +b.
Lastly for  , we
will look at the graph when a > b.
, we
will look at the graph when a > b.
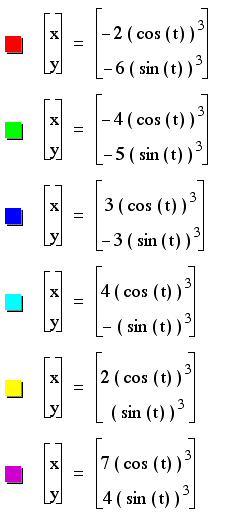
 Again, the same is true for a <
b and a > b when the parametric equation is of the form
Again, the same is true for a <
b and a > b when the parametric equation is of the form  .
.
Now, let's examine one more parametric
equation of the form  so that we can
be sure when we make our generalizations about parametric equations
of this form.
so that we can
be sure when we make our generalizations about parametric equations
of this form.

 This is similar to the parametric equation
of the form
This is similar to the parametric equation
of the form  , only now we have curves instead
of segments. But, the fact that y-intercept = x-intercept = a
= b remains the same.
, only now we have curves instead
of segments. But, the fact that y-intercept = x-intercept = a
= b remains the same.
Let's now take a look at  for a < b.
for a < b.

 This is also similar to
This is also similar to  for a < b. Again, we have curves instead of segments, but y-intercept
= b, and x-intercept = a.
for a < b. Again, we have curves instead of segments, but y-intercept
= b, and x-intercept = a.
Lastly, we observe  for a > b.
for a > b.

 Again, we see the similarity to
Again, we see the similarity to  .
.
CONCLUSION
After observing these graphs, I would
like to make some generalizations:
1. Parametric equations of the form  have the following characteristics:
have the following characteristics:
M = 2 : A Special Case:
- Segments will form with slope =
 ,
y-intercept = b, and x-intercept = a.
,
y-intercept = b, and x-intercept = a.
M Even:
- Curves will from with y-intercept = b, and
x-intercept = a.
M = 1 : A Special Case:
- When a = b circles will form with radius
=
 .
.
- When
 , ellipses will
form with the major axis equal to the greater of
, ellipses will
form with the major axis equal to the greater of or
or and the minor axis equal to the smaller.
and the minor axis equal to the smaller.
M Odd:
- Diamond-like shapes form with curved lines
and x-intercept = +a and y-intercept = +b.
Return
 ,
,  ,
,  , etc.
, etc. ,
,  ,
,  , etc.
, etc. .
.

 .
.

 .
.

 for a = b.
for a = b.

 .
.

 .
.

 , the graphs when a < b have
the same characteristics of the graphs when a > b.
, the graphs when a < b have
the same characteristics of the graphs when a > b. for a = b.
for a = b.

 for a < b.
for a < b.

 , we
will look at the graph when a > b.
, we
will look at the graph when a > b.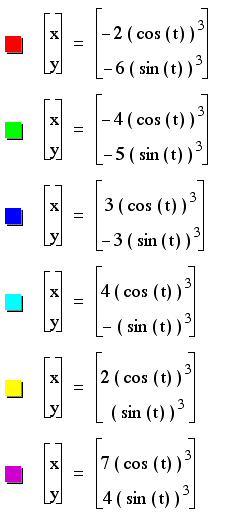

 .
. so that we can
be sure when we make our generalizations about parametric equations
of this form.
so that we can
be sure when we make our generalizations about parametric equations
of this form.

 , only now we have curves instead
of segments. But, the fact that y-intercept = x-intercept = a
= b remains the same.
, only now we have curves instead
of segments. But, the fact that y-intercept = x-intercept = a
= b remains the same. for a < b.
for a < b.

 for a < b. Again, we have curves instead of segments, but y-intercept
= b, and x-intercept = a.
for a < b. Again, we have curves instead of segments, but y-intercept
= b, and x-intercept = a. for a > b.
for a > b.

 .
. have the following characteristics:
have the following characteristics: