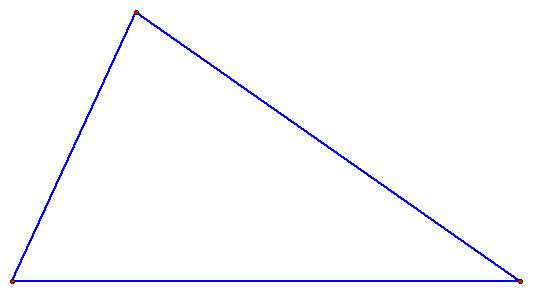
TRIANGLE 1

ORIGINAL TRIANGLE
TRIANGLE 2
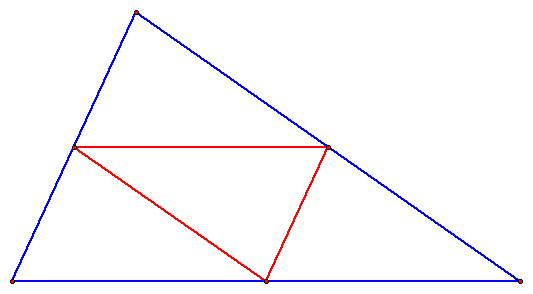
MEDIAL TRIANGLE
TRIANGLE 3
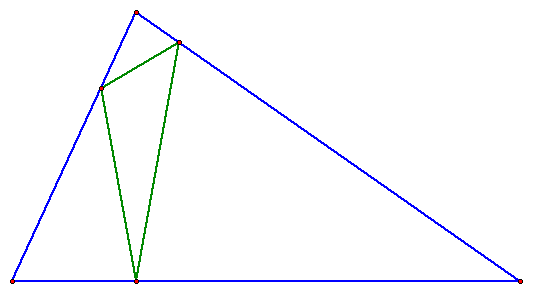
ORTHIC TRIANGLE
TRIANGLE 4
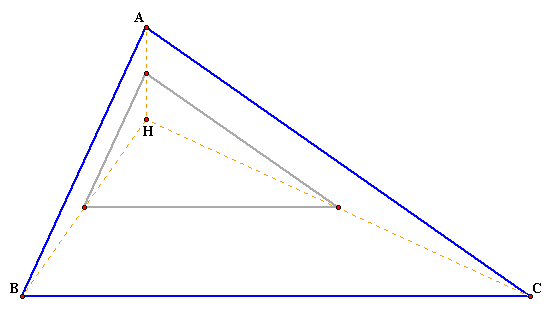
H is the orthocenter of TRIANGLE 1.
The vertices of TRIANGLE 4 are found by
taking the midpoints of HA, HB, and HC.
Now, let's find the circumcircle of TRIANGLE 2, TRIANGLE 3, and TRIANGLE 4.
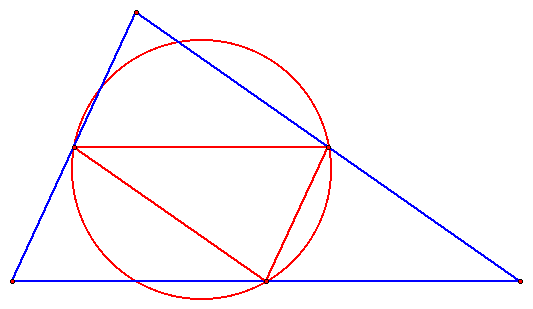 TRIANGLE 2
TRIANGLE 2
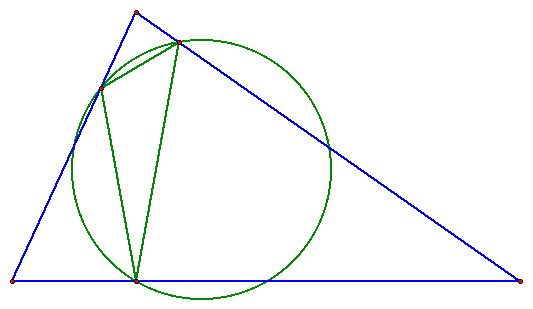 TRIANGLE 3
TRIANGLE 3
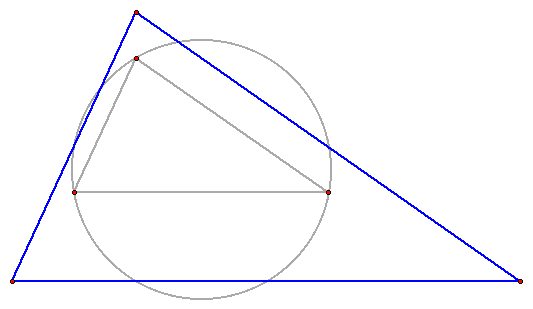 TRIANGLE 4
TRIANGLE 4
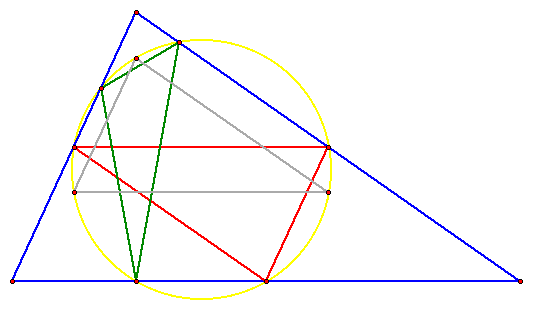
Recall how a circumcircle is formed. It is the circle whose center is the circumcenter of the triangle in question. The circumcenter is the intersection of all of the perpendicular bisectors of each leg of the triangle.
For example, the circumcenter, X, of TRIANGLE 3 would be found like so:
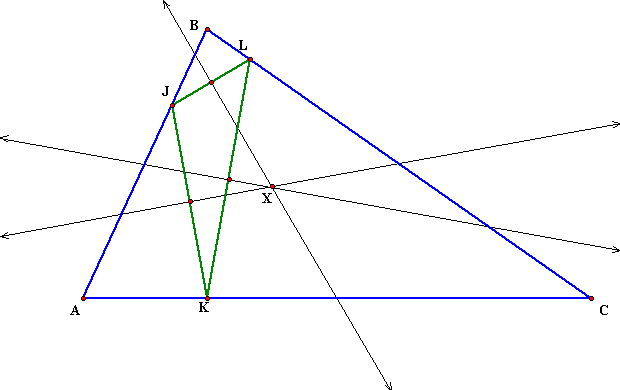
Now, let's look at the circumcenter of all the triangles.
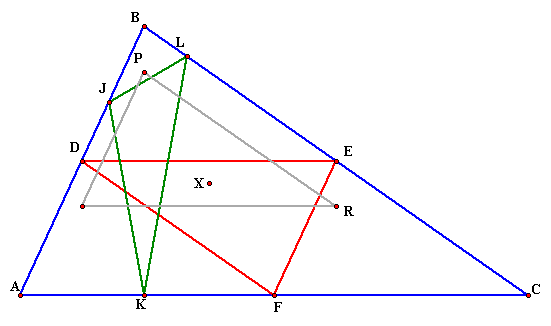
TA-DA! This explains why all of the circumcircles
are the same, they all share the same circumcenter!
It is also interesting to note that in constructing these three secondary triangles and their circumcircle, we have also constructed the nine-point circle for TRIANGLE 1.
The nine-point circle for any triangle passes through the three mid-points of the sides, the three feet of the altitudes, and three mid-points of the segments from the respective vertices to the orthocenter.
By definition, the nine-point circle is made
up of the vertices of each secondary triangle that we constructed
here!