Graph the following: x² + y² = 1

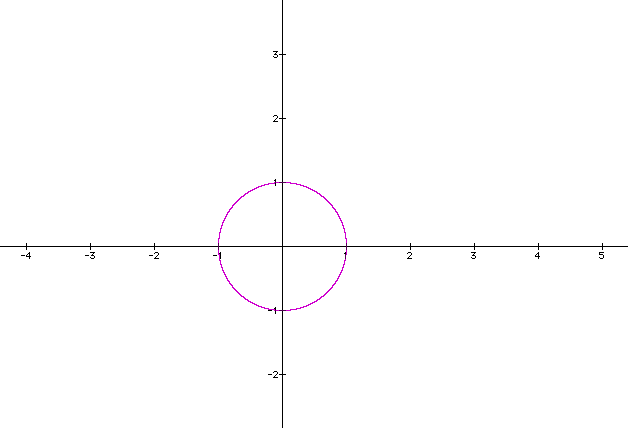
Notice the circle has a radius of 1. It is a regular shape.

Now examine the graph: x³ + y³ = 1

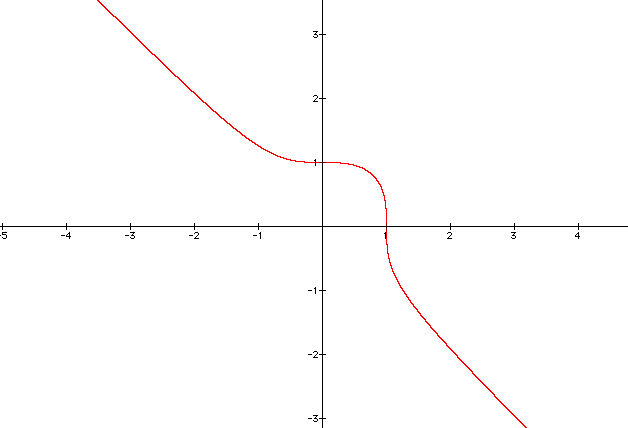
The equation has now changed from a circle to a line with a rounded shape between the coordinates (-1,1) and (1,-1).

Let's increase the exponents again and graph x⁴ + y⁴ =1

The graph now exhibits the shape of a square with s=1.

How will an exponent of 5 changed the graph?

Let's examine it. Graph x⁵ + y⁵ = 1.

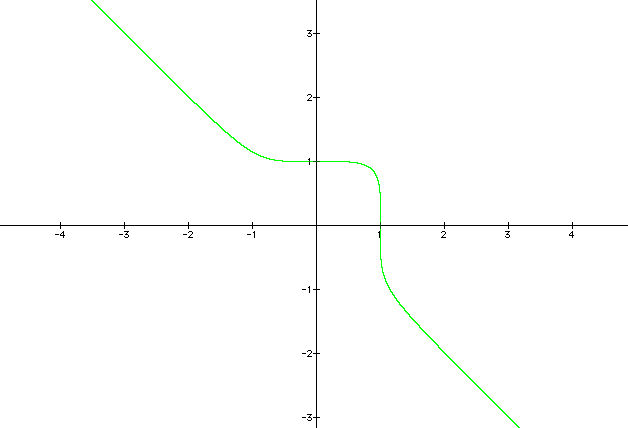
The graph now looks very similar to x³ + y³ = 1. It is a line with an interruption around (-1, 1) and (1, -1).

Now lets examine all the graphs together.

x² + y² = 1

x³ + y³ = 1

x⁴ + y⁴ =1

x⁵ + y⁵ = 1

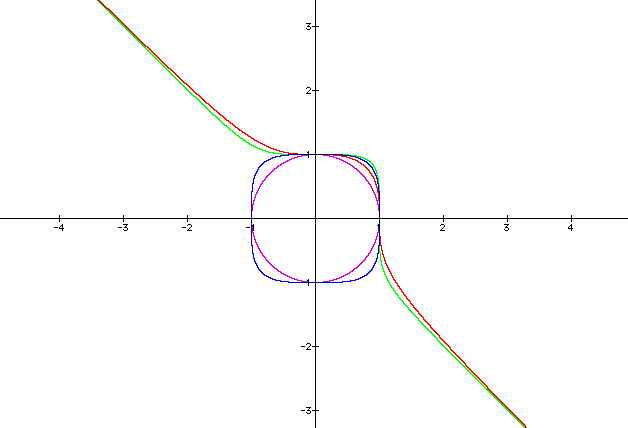
Notice the points at x = 1, -1 and y = 1, -1. What can you assume from the graph of x²⁴ + y²⁴ =1? Or x²⁵ + y²⁵ =1?

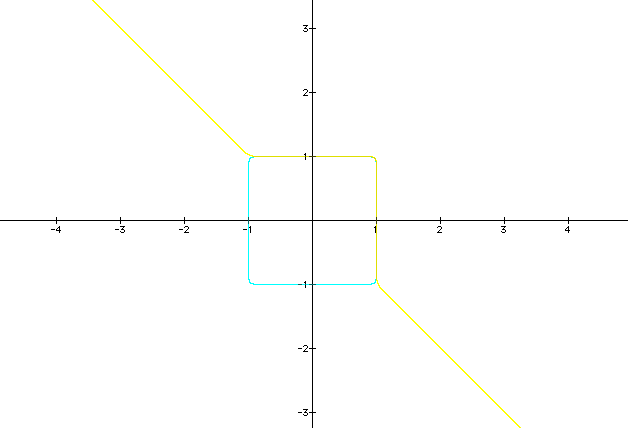
Lets try even higher exponential values.

x¹⁰⁰ + y¹⁰⁰ =1

x¹⁰¹ + y¹⁰¹ =1

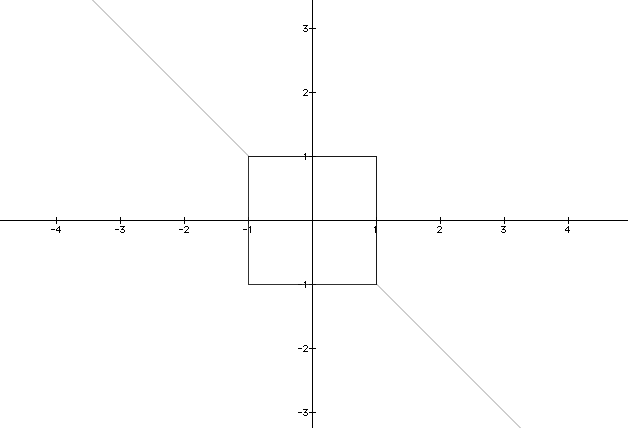
We can now justify an assumption that as the exponents get higher the image becomes sharper.

Return to MBauers 6680 Home Page