

This assignment is about polar equations. We will examine the equation of
Let us first examine the effects of theta . We will keep a, b, and k constant.
CASE #1
a = 0
b and k = 1
We will start with theta ranging from 0 to 6.28.
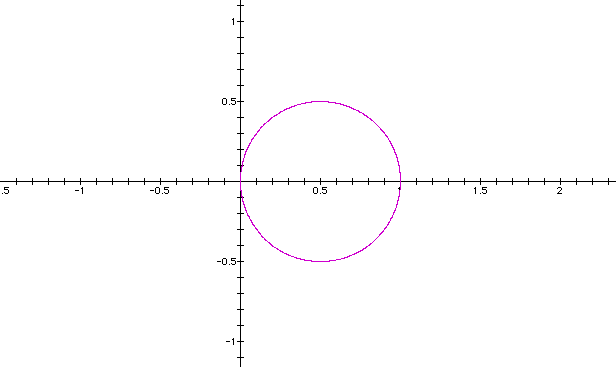
CASE #2
Now we will vary k.
k = 2
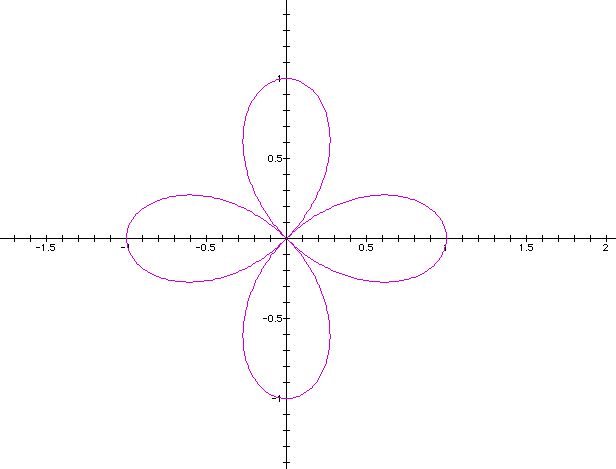
k = 3
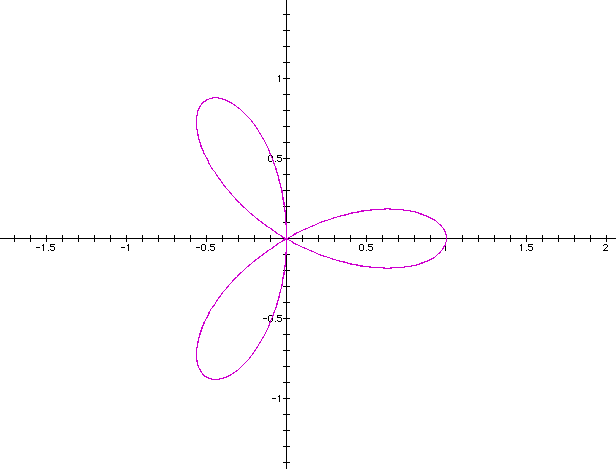
k = 4
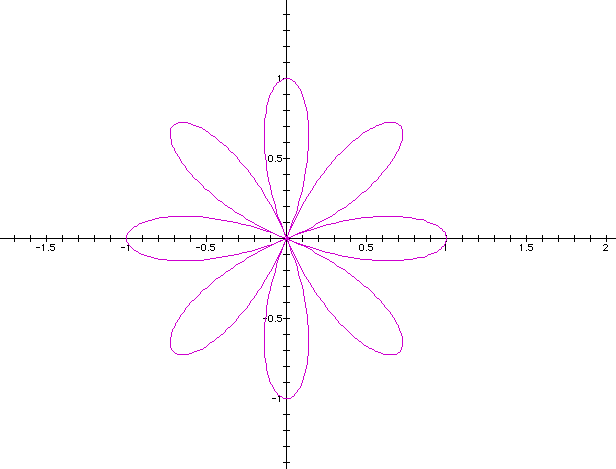
k = 5
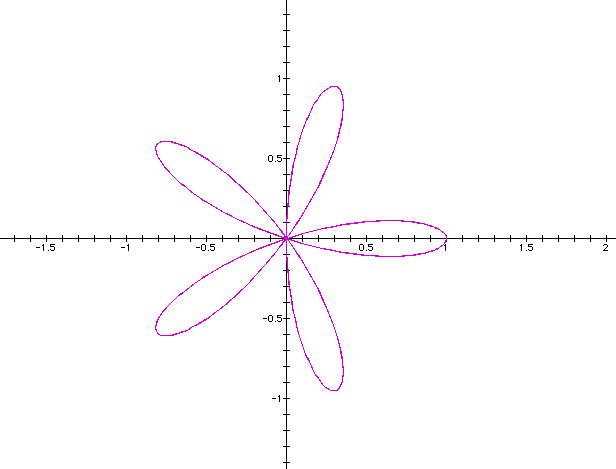
As the value of k changes the number of leafs on the graph change. Click on link for a dramatic animation of k ranging from -25 to 25. Notice in the animations the negative numbers give the same picture as the positive.
CASE #3
Vary the values of b.
a = 0
k = 1
Let us start with b = 2. We will overlay onto the graph when b = 1.
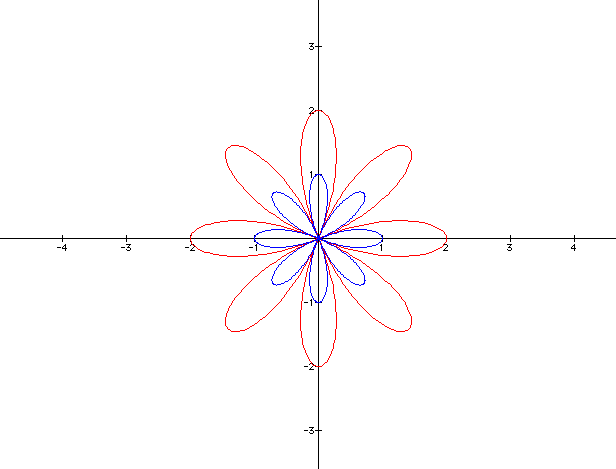
b = 5
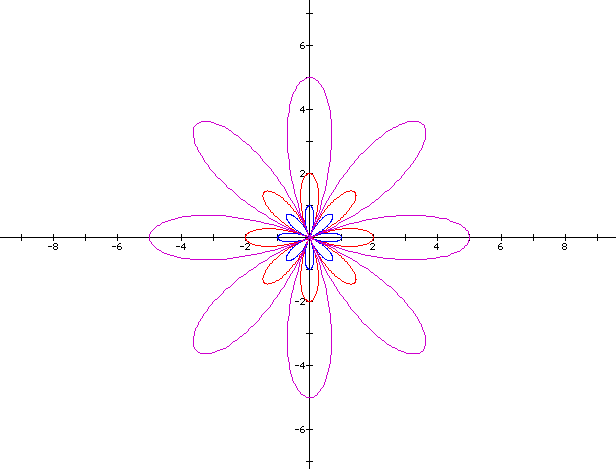
Notice changing b increases the size of the leafs. Click here for an animation of b going from -4 to 4. Notice in the animation the negative numbers give the same picture as the positive.
CASE #4
We will go back to k =4, b = 1, and a will vary.
a =1
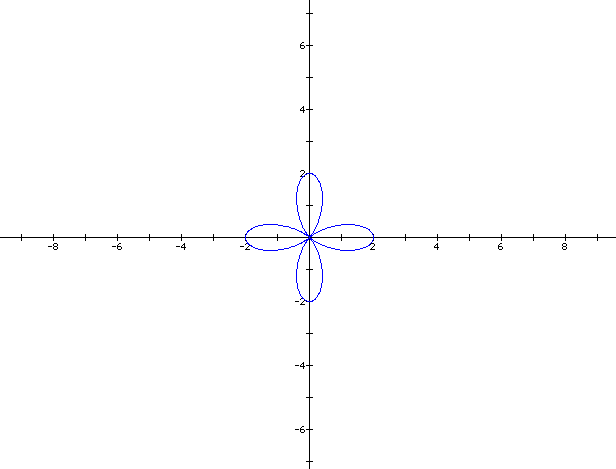
a = 2
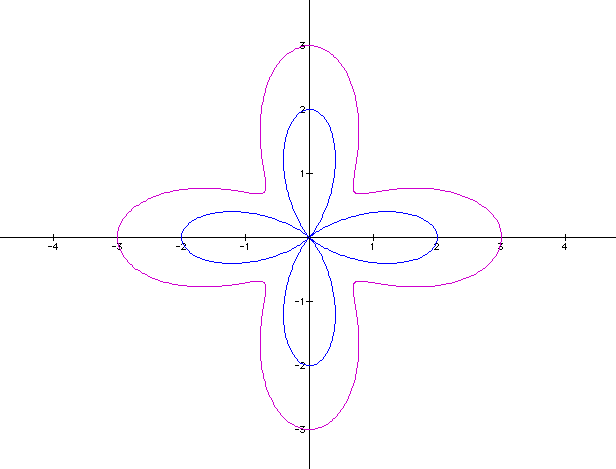
a = 3
When a varies the "leaf rose" formation changes. Click below for an animation of a changing from -8 to 8. Notice the negative numbers look the same as the positive numbers.
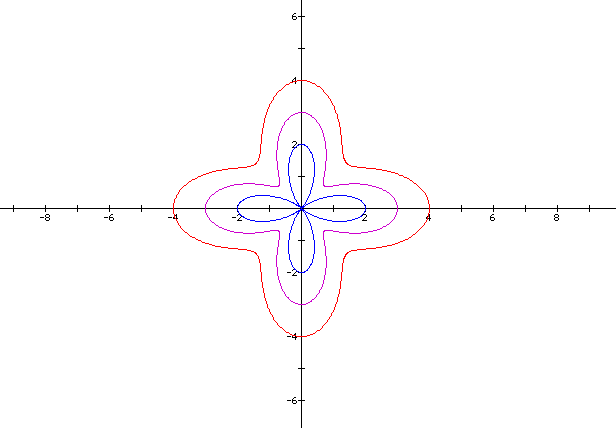
SPECIAL CASE
When a and b are the same the graphs are called cardiods. If a does not equal b, then graph is called a limacon. Here are some examples:
a = 1
b = 2
k = 1
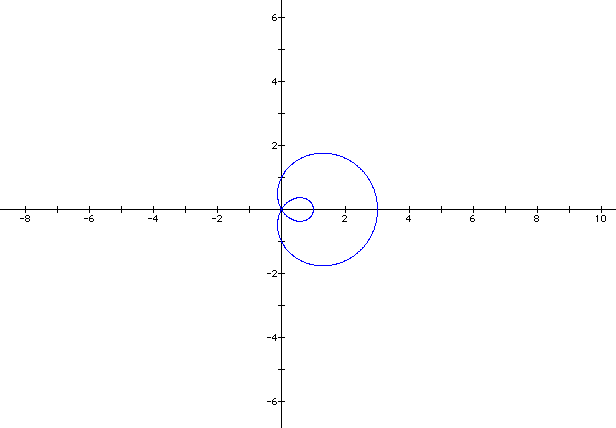
a = 1
b = -2
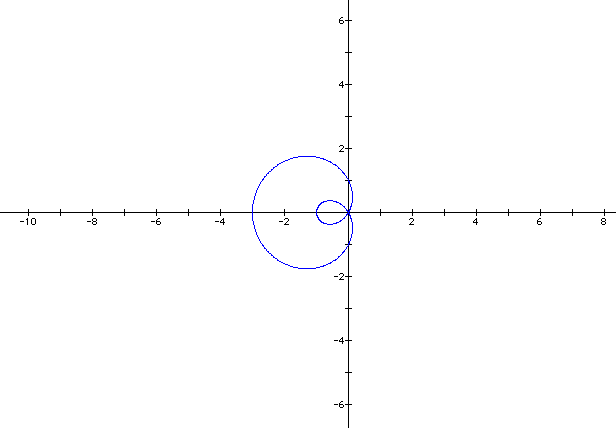
a = 3
b = 2
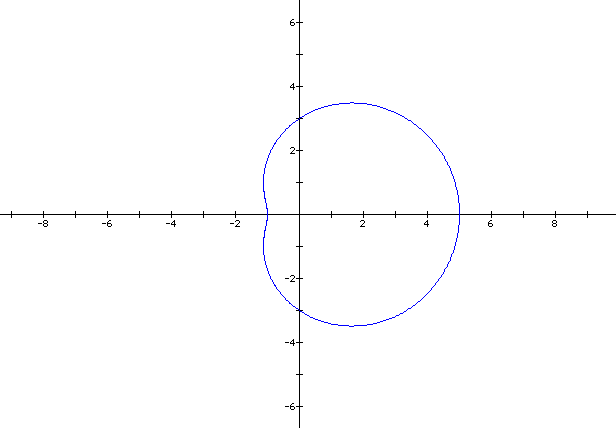
As the difference of a and b increases when a > b and b does not equal to 0, the graph resembles a circle. As the difference of a and b increases when b > a and a does not equal to 0, then the inner circle becomes bigger.
Click here for a = 10 and b = 1.
Click here for a =1 and b =10.