

The Fibonnaci Sequence is the sequence of 1, 1, 2, 3, 5, 8, 13, … It is generated by taking the sum of the two previous terms. The equation is f(n) = f(n-1) + f(n-2).
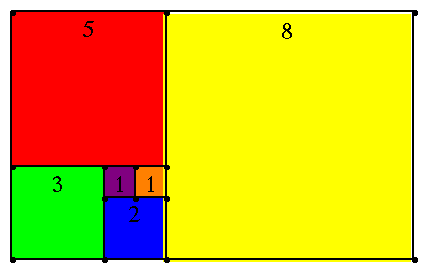
This is a example of a Fibonnaci Square. Each color represents a number in the sequence. In this assignment, we will look at the Fibonnaci Sequence using a spreadsheet.
| n | f(n)=f(n-1) + f(n-2) |
|
0 |
1 |
|
1 |
1 |
|
2 |
2 |
|
3 |
3 |
|
4 |
5 |
|
5 |
8 |
|
6 |
13 |
|
7 |
21 |
|
8 |
34 |
|
9 |
55 |
|
10 |
89 |
|
11 |
144 |
|
12 |
233 |
|
13 |
377 |
|
14 |
610 |
|
15 |
987 |
|
16 |
1597 |
|
17 |
2584 |
|
18 |
4181 |
|
19 |
6765 |
|
20 |
10946 |
|
21 |
17711 |
|
22 |
28657 |
|
23 |
46368 |
|
24 |
75025 |
|
25 |
121393 |
|
26 |
196418 |
|
27 |
317811 |
|
28 |
514229 |
|
29 |
832040 |
|
30 |
1346269 |
|
31 |
2178309 |
|
32 |
3524578 |
|
33 |
5702887 |
|
34 |
9227465 |
|
35 |
14930352 |
|
36 |
24157817 |
|
37 |
39088169 |
|
38 |
63245986 |
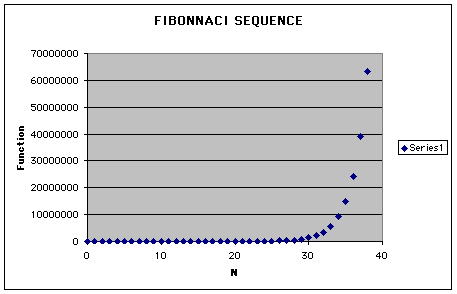
As n increases the f(n) becomes increasingly bigger. Notice the sharp curve of the graph. Now let's look at the ratio of the second term compared to the first.
Now let us examine the ratio of terms.
| n | f(n)=f(n-1) + f(n-2) | Ratio of f(n)/f(n-1) | Ratio of f(n)/f(n-2) | Ratio of f(n-1)/f(n-2) |
|
0 |
1 |
|||
|
1 |
1 |
1 |
||
|
2 |
2 |
2 |
2 |
1 |
|
3 |
3 |
1.5 |
3 |
2 |
|
4 |
5 |
1.666666667 |
2.5 |
1.5 |
|
5 |
8 |
1.6 |
2.66666667 |
1.666666669 |
|
6 |
13 |
1.625 |
2.6 |
1.6 |
|
7 |
21 |
1.615384615 |
2.625 |
1.625 |
|
8 |
34 |
1.619047619 |
2.615384615 |
1.615384615 |
|
9 |
55 |
1.617647059 |
2.619047619 |
1.619047619 |
|
10 |
89 |
1.618181818 |
2.617647059 |
1.617647059 |
|
11 |
144 |
1.617977528 |
2.618181818 |
1.618181818 |
|
12 |
233 |
1.618055556 |
2.617977528 |
1.617977528 |
|
13 |
377 |
1.618025751 |
2.618055556 |
1.618055556 |
|
14 |
610 |
1.618037135 |
2.618025751 |
1.618025751 |
|
15 |
987 |
1.618032787 |
2.618037135 |
1.618037135 |
|
16 |
1597 |
1.618034448 |
2.618032787 |
1.618032787 |
|
17 |
2584 |
1.618033813 |
2.618034448 |
1.618034448 |
|
18 |
4181 |
1.618034056 |
2.618033813 |
1.618033813 |
|
19 |
6765 |
1.618033963 |
2.618034056 |
1.618034056 |
|
20 |
10946 |
1.618033999 |
2.618033963 |
1.618033963 |
|
21 |
17711 |
1.618033985 |
2.618033999 |
1.618033999 |
|
22 |
28657 |
1.61803399 |
2.618033985 |
1.618033985 |
|
23 |
46368 |
1.618033988 |
2.61803399 |
1.61803399 |
|
24 |
75025 |
1.618033989 |
2.618033988 |
1.618033988 |
|
25 |
121393 |
1.618033989 |
2.618033989 |
1.618033989 |
Notice the ratio of terms in column 3. They come out to be the golden ration. The ratios in columns 4 and 5 follow suit.
The next series will start out with different values for f(0) and f(1). The Lucas Sequence starts as f(0) = 1 and f(1) =3. Now look at the ratios.
| n | f(n)=f(n-1) + f(n-2) | Ratio of f(n)/f(n-1) | Ratio of f(n)/f(n-2) | Ratio of f(n-1)/f(n-2) |
|
0 |
1 |
|||
|
1 |
3 |
3 |
||
|
2 |
4 |
1.333333333 |
4 |
3.000000001 |
|
3 |
7 |
1.75 |
2.33333333 |
1.333333331 |
|
4 |
11 |
1.571428571 |
2.75 |
1.75 |
|
5 |
18 |
1.636363636 |
2.571428571 |
1.571428571 |
|
6 |
29 |
1.611111111 |
2.636363636 |
1.636363636 |
|
7 |
47 |
1.620689655 |
2.611111111 |
1.611111111 |
|
8 |
76 |
1.617021277 |
2.620689655 |
1.620689655 |
|
9 |
123 |
1.618421053 |
2.617021277 |
1.617021277 |
|
10 |
199 |
1.617886179 |
2.618421053 |
1.618421053 |
|
11 |
322 |
1.618090452 |
2.617886179 |
1.617886179 |
|
12 |
521 |
1.618012422 |
2.618090452 |
1.618090452 |
|
13 |
843 |
1.618042226 |
2.618012422 |
1.618012422 |
|
14 |
1364 |
1.618030842 |
2.618042226 |
1.618042226 |
|
15 |
2207 |
1.618035191 |
2.618030842 |
1.618030842 |
|
16 |
3571 |
1.61803353 |
2.618035191 |
1.618035191 |
|
17 |
5778 |
1.618034164 |
2.61803353 |
1.61803353 |
|
18 |
9349 |
1.618033922 |
2.618034164 |
1.618034164 |
|
19 |
15127 |
1.618034014 |
2.618034014 |
1.618033979 |
|
20 |
24476 |
1.618033979 |
2.618033979 |
1.618033992 |
|
21 |
39603 |
1.618033992 |
2.618033992 |
1.618033987 |
|
22 |
64079 |
1.618033987 |
2.618033987 |
1.618033989 |
|
23 |
103682 |
1.618033989 |
2.618033989 |
1.618033988 |
|
24 |
167761 |
1.618033989 |
2.618033989 |
1.618033989 |
|
25 |
271443 |
1.618033989 |
2.618033989 |
1.618033989 |
The ratios converge to the golden ratio. This convergence does not require f(n) to start at a certain value.