Let us begin Assignment #8 with the construction of triangle ABC.

Now we will construct the Orthocenter H of triangle ABC.

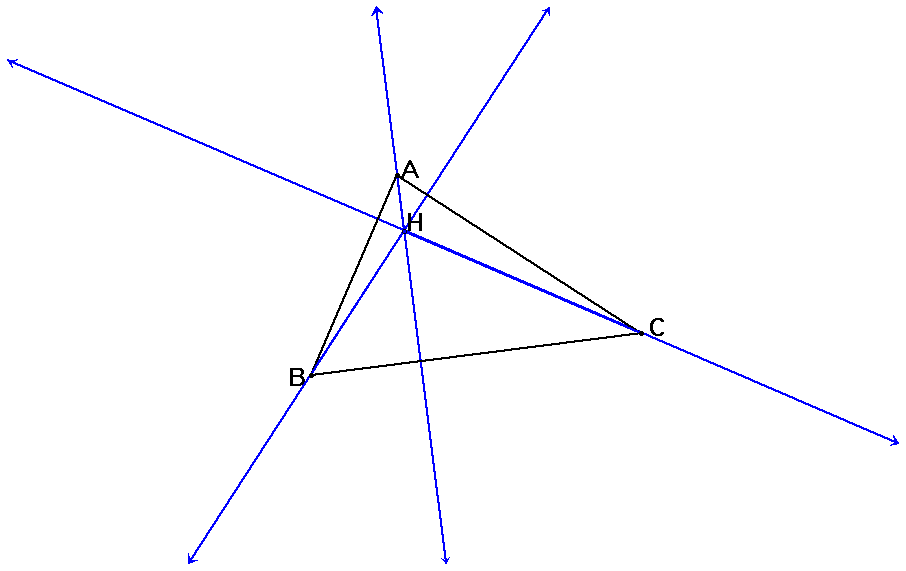
Now let us view the contruction of triangle HBC and its orthocenter.

The Orthocenter of triangle HBC lies on Point A of the original triangle ABC. Explore further with GSP Triangle HBC.gsp

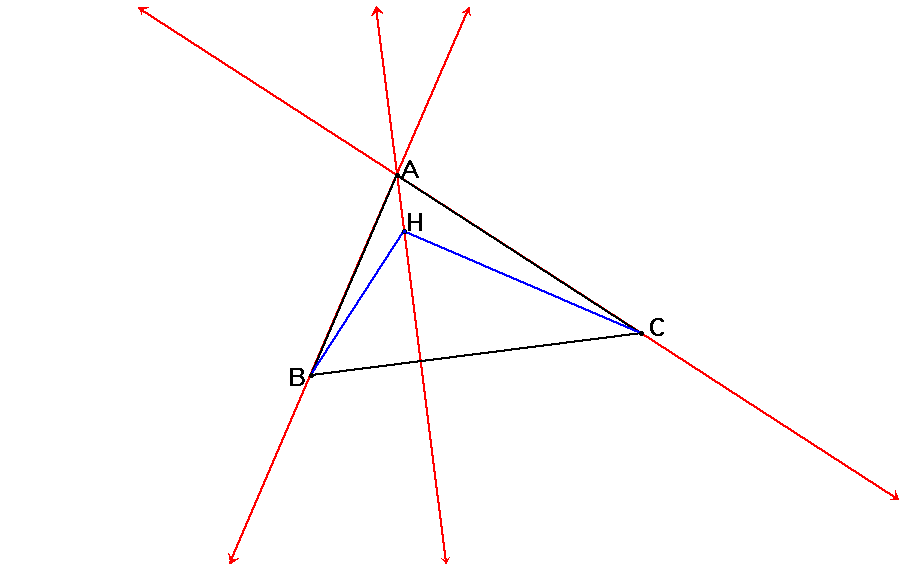
We will continue our exploration with the construction of the Orthocenter for triangle HAB (which is at point C)

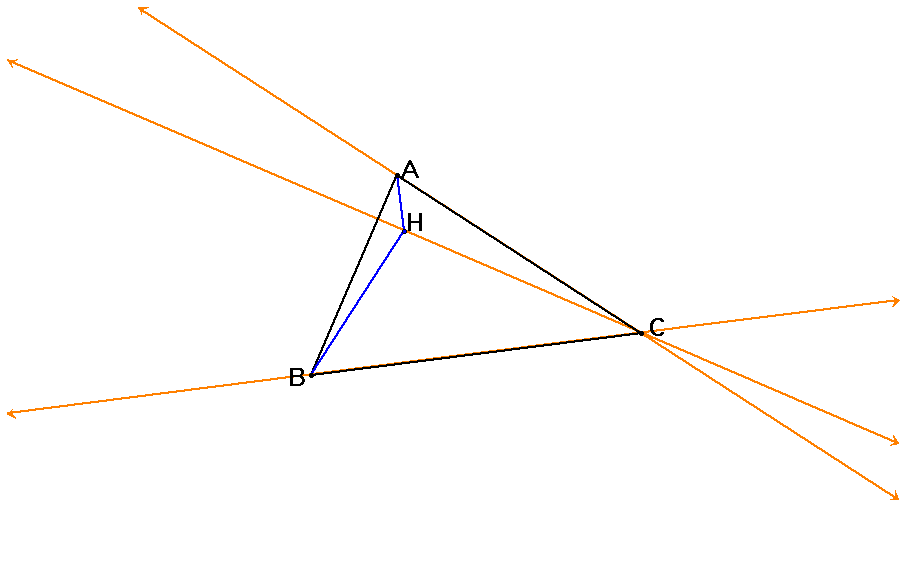
and triangle HAC (which is at Point B).

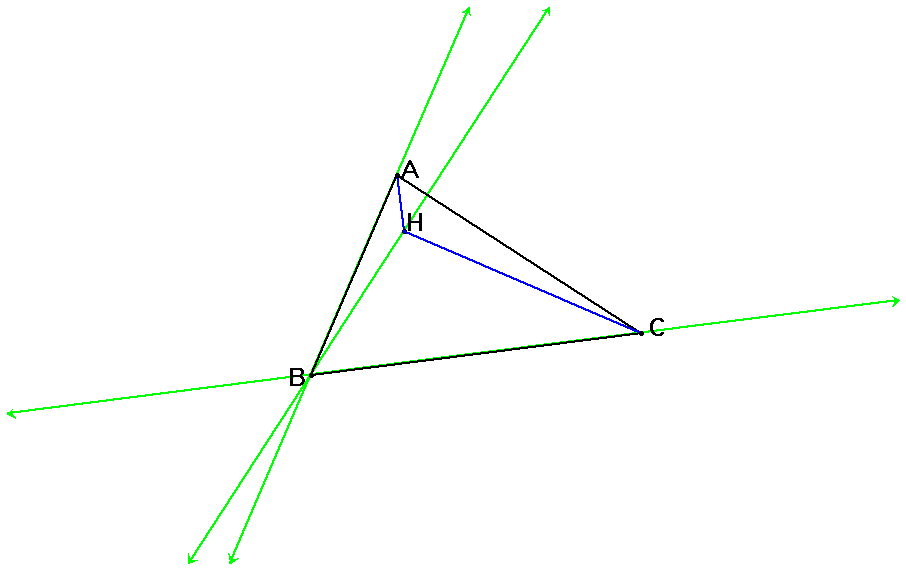
Now we will construct the circumcircles of triangles ABC, HBC, HAB, and HAC.

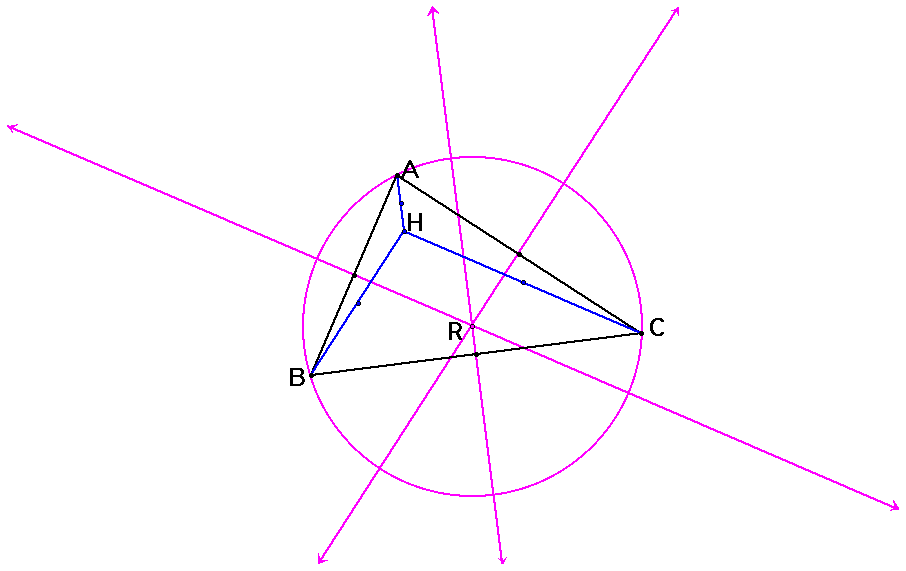
R is the circumcenter of triangle ABC.

S is the circumcenter of triangle HBC. It lies along the midpoint of line BC and the circumcenter of triangle ABC which is point R.

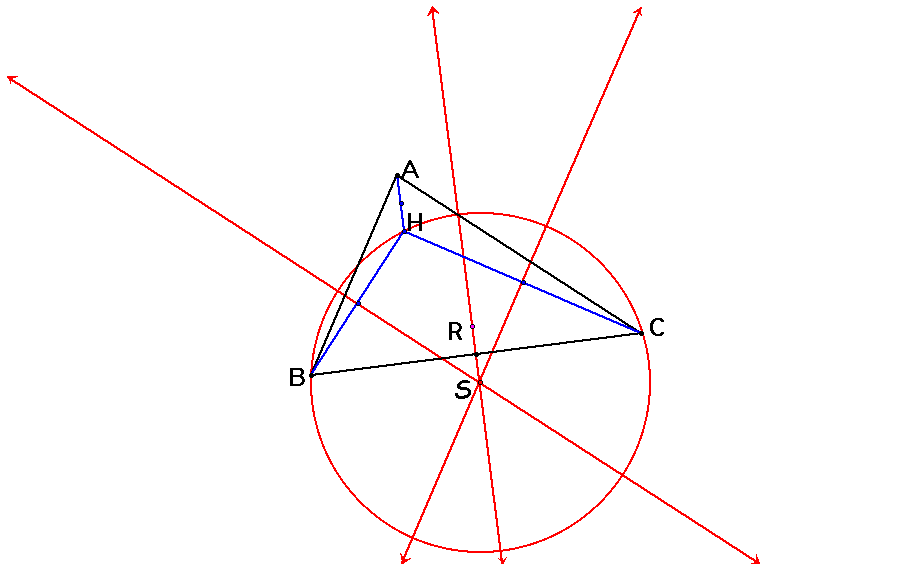
T is the circumcenter of triangle HAB. It lies along the line of the midpoint of line AB and the circumcenter of triangle ABC which is Point R.

U is the circumcenter of triangle HAC. U lies along the midpoint of line AC and Point R.

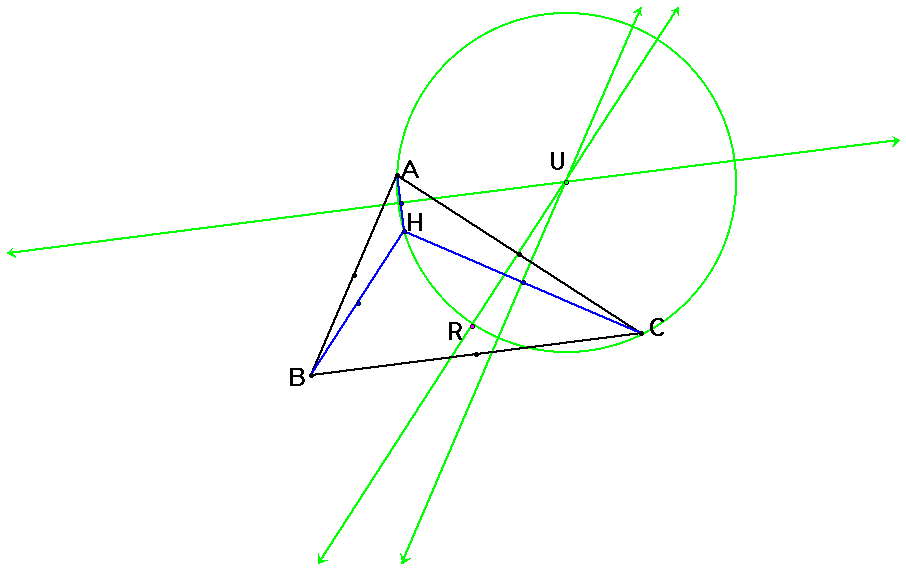
We will continue with Assignment #8 by using various links and constructions.

 Now let's construct the nine point circle for triangles ABC, HBC, HAC, and HAB. Nine Point Circles

 This link will explore triangle ABC and its incircle, its three excircles and its nine-point circle. Assin#8triangleABC.html

 This construction views the orthic triangle and its relationship to the altitudes and the circumcircle. Assn#8OrthicTriangle.html

 Proof for Orthocenter and its perpendiculars. Assn #8 Orthocenter.html

 Construction and exploration for internal angle bisectors. Assn#8 Internal Angle Bisectors.html

 Reflections with respect to triangle ABC, its orthocenter, and circumcircle for triangle ABH. Reflections of Triangle ABC.html

 Find the minimal perimeter of a triangle inscribed in a given triangle. Assn #8 Problem.html

Return to MBauers 6680 Home Page