
Lesson 6:
Applications
of Conics
By Carly
Coffman

Comet &
Planet Orbits
Of the 610
comets identified prior to 1970,
Ø
245 have elliptical orbits
Ø
295 have parabolic orbits
Ø
70 have hyperbolic orbits
(Algebra and Trigonometry, Larson &
Hostetler 2001)
As you will
see in the following pictures, planets also have elliptical orbits.
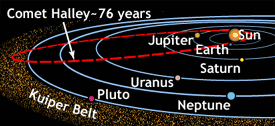
One example of an elliptical orbit is the famous Halley’s
Comet.
It takes a period of 76
years to complete it’s orbit.

A recent comet named
“Linear” has a parabolic orbit.
1) Why would the path of comets be of any interest to you and
me?
|
Planet |
Period |
|
|
|
|
(yr) |
|
|
|
|
|
Mercury |
0.241 |
|
Venus |
0.615 |
|
Earth |
1 |
|
Mars |
1.88 |
|
Jupiter |
11.8 |
|
Saturn |
29.5 |
|
Uranus |
84 |
|
|
165 |
|
Pluto |
248 |
|
|
|
Here is a table for the
period (length of time for a planet to complete one orbit around the sun) of
each planet. (The mathematics behind
planetary orbit can be found at http://www.glenbrook.k12.il.us/gbssci/phys/Class/circles/u6l4a.html)
Eccentricity
*You may work the problems
on this application page on notebook paper. Make sure that you show your work and that you
write neatly.
The eccentricity determines
the shape of the object path. Here is a
table for eccentricity values:

The eccentricity of a
planet with an elliptical orbit is defined by e = c/a where e is the
eccentricity, a is half of the minor axis, and c is
found by c^2 = a^2 – b^2 (where b is the length of half of the minor axis and c
is the distance from the center to each focus).
2) The planet Pluto moves in an elliptical
orbit with the sun at one of the foci. The
length of half of the major axis, a, is 3.666 x 10^9 miles and the eccentricity
is 0.248. Find the smallest distance and
the greatest distance of Pluto from the center of the sun. (Draw a diagram)
*From Algebra and Trigonometry , Larson & Hostetler, 2001
Return to Home Page Next Lesson