
Lesson
2:
The
Ellipse
By
Carly Coffman
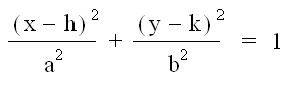
During this
lesson we will explore the equation of an ellipse so that you will be able to
recognize and manipulate it when you come in contact with it.
Open a
Microsoft Word document, title it “Ellipse” and type your name and period under
the title. You will use this to answer
any questions given in this lesson.
Remember to use complete sentences on all answers. You do not have to type the questions. Also, feel free to add comments and findings
to the questions.
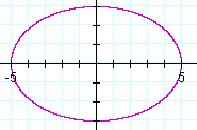
First, let’s
look at an ellipse.
Terms: An axis is the line of symmetry that runs vertical or
horizontal in the ellipse. The longer
axis is called the major axis while the shorter axis is called the minor axis.

In
this ellipse, if each tick mark represents one, the major axis has a length of
10 and the minor axis has a length of 6.
Now, we are
going to manipulate some values in the equation to explore the equation of an
ellipse. Go back to the previous link
and change the number “3” to a lower case “n”.
(If you do not see an equation put your cursor at the top edge of the
graphing screen where it becomes two lines.
Then, click and drag down. You
should see a screen with an equation.)
Next, in the bottom left corner of the same graphing calculator screen
click on n and make the window look
like the following window.
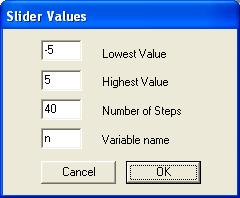
Click on the
play button on the bottom of the screen and watch what happens when n is
changed. On your Word document answer
the following question.
1)
What
variable is n connected with and how?
2)
How does
changing n affect the ellipse?
Next, we
will explore the constant connected with y.
So, use the following link to explore the constant, which will also be
n.
3)
Explain what
the relationship is between this n and the
ellipse.
Well, this
is a bit confusing! We have two n’s. Let’s give each one a different name so that
you will know which n I am referring to later in the lesson. The first n we
studied will be h. The second n we
studied will by k.
4)
Explain how
to tell the difference between h and k when
looking
at an equation for an ellipse.
Now, choose
an h and k so that the ellipse is centered at the origin as shown below.
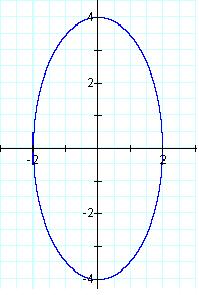
5)
Record what
h and k have to be in order for the ellipse to be centered at the origin. Also record the entire equation for this
ellipse. Now, double click on the
picture above, copy it, and paste it into your Word document next to the
equation you created.
Next, let’s
look at manipulating the denominators of the equation. We will use an ellipse
with a center of (0,0). Notice what happens as the
denominator of the x-variable increases.
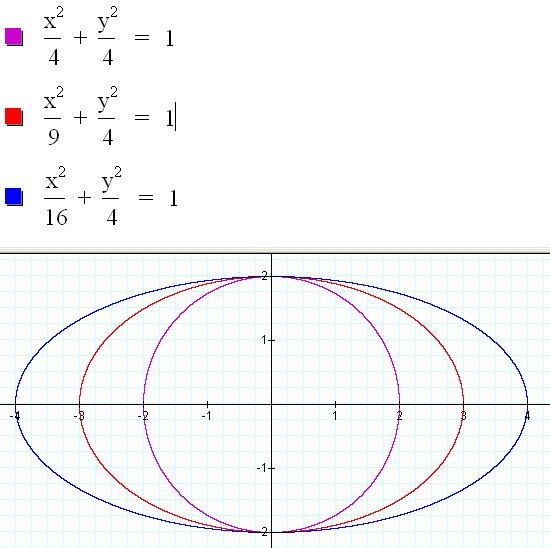
6)
Create a
table of values with the denominator of the x-variable and the length
of
the major axis. What is the
relationship?
Open the
following link and click on the play button at the bottom to see how the
ellipse changes when the denominator of the y-variable is manipulated.
7)
Create a
table of values with the denominator of the y-variable and the length of the
ellipse on the y-axis. Use perfect
squares for values of the denominator.
What is the relationship?
8)
What happens
when you use a negative value for either denominator? Is the
figure
still an ellipse? If not, what type of
figure is it?
Now, let’s
put our investigations together. Copy
and paste the following equation into your Word document.
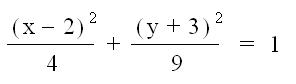
Find each of
the following for the equation above.
9) Center: ( __, ___ )
Length of the ellipse on the
x-axis:
Length of the ellipse on the
y-axis:
Foci
An ellipse
is the set of all points (x,y)
in a plane the sum of whose distances from two distinct fixed points (foci) is
constant. You can create your own
ellipse by tying string to two thumbtacks, taking a pencil and stretching the
string, and drawing around the thumbtacks so that the string is always tight.
The foci are
found by using the equation, ![]() , where c
is the distance from the center of the ellipse to each focus. The coordinates of the foci
are (h-c, k) and (h+c, k) if the major axis is
horizontal and (h, k-c) and (h, k+c) if the major
axis is vertical.
, where c
is the distance from the center of the ellipse to each focus. The coordinates of the foci
are (h-c, k) and (h+c, k) if the major axis is
horizontal and (h, k-c) and (h, k+c) if the major
axis is vertical.
Let’s look
at an example.
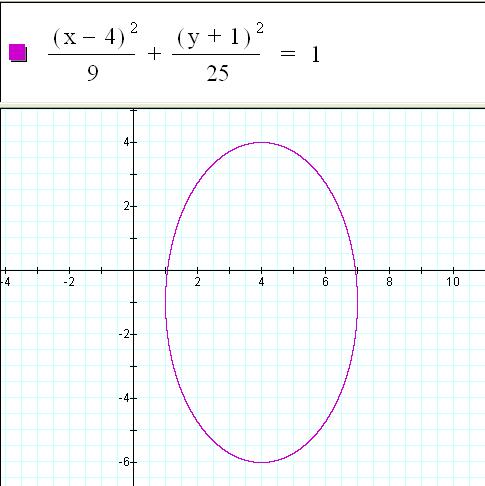
The
center here is (4,-1). The major axis is
10 units long, so a must be 5. The minor
axis is 6 units long, so b must be 3. We
can substitute these values into the equation, ![]()
![]()
![]()
![]()
The
foci always lie on the major axis and are c units away from the center. So, the foci are (4, -1+4) and (4, -1-4),
which is (4, 3) and (4, -5).
In your word
document add the foci for the equation in #9.
*Make sure
your name is on your Word document and print it. Place this document with your conic document
in your portfolio or notebook. You are
finished with the ellipse lesson!
Return to
Mrs. Coffman’s Webpage Next
Lesson