In this assignment we will consider any triangle ABC and the following construction. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

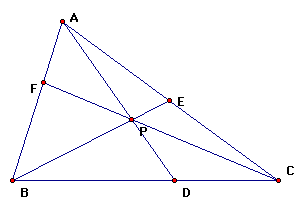
We will explore the relationship of (AF)(BD)(EC) to (FB)(DC)(EA).

We will also explore P inside and outside of the triangle.

Use the link above to explore the triangle ABC and the point P.

Conjecture 1: (AB)(BD)(EC) = (FB)(DC)(EA)

• To explore triangle with measurements of the sides click here.

Proof (attempts): I could not come up with a proof of why conjecture 1 is true. Here were a few of my attempts on how to do it.

Attempt 1: Draw parrallel lines to side AB at points A and C. Then, construct the other half of the parallelogram that is twice the area of triangle ABC by constructing parallel lines to segment CF at points A, F, and B. I saw that triangle AFP is one-fourth the area of the top parallelogram. Then, I came to a dead end. Here is my sketch.

Attempt 2 (better of the two): Draw parallel lines to segment CF at points A and B.

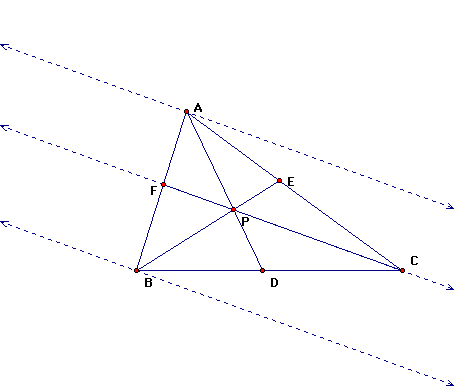
Then, angle EPA is congruent to angle BPD by vertical angles.

*Angle APB is congruent to angle EPD by vertical angles.

**Angle FPB is congruent to angle EPC by vertical angles.

Angle CPD is congruent to angle APF since * and **.

Since these angles are congruent, segment BF is in proportion to segment EC, segment AF is in proportion to segment CD, and segment AE is in proportion to segment DB.

The proportions should work out so that (AB)(BC)(EC)=(FB)(DC)(EA).

Here is a sketch for exploring this attempt.

Conjecture 2: When P is located on the centroid of triangle ABC, the ratio of the areas of triangle ABC to triangle DEF is exactly four.

• Click here to explore special case where ratio = 4

Proof : We will first draw some auxillary lines to show that triangle EDF is one-fourth the area of triangle ABC. First, create parallel lines to segment DF at points B and C. Next, create parallel lines to segment EF at points B and A.

Now, we can observe congruent angles.

Angle EFD is congruent to angle FDB by alternate interior angles.

Angle EDF is congruent to angle DFB by alternate interior angles.

Side DF is congruent to itself by the reflexive property.

Thus, triangle FDB is congruent to triangle DFE by ASA.

Angle AEF is congruent to angle EFD by alternate interior angles.

Angle EAF is congruent to angle AFG by alternate interior angles.

Angle AFG is congruent to angle EDF by corresponding angles.

So, angle EAF is congruent to angle EDF.

Side EF is congruent to itself by the reflexive property.

Thus, triangle AEF is congruent to triangle DFE.

Angle EDC is congruent to angle DEF by alternate interior.

Segment DE is congruent to segment DE by the reflexive property.

Angle CED is congruent to angle EDF by alternate interior angles.

Thus, triangle CED is congruent to triangle FDE by ASA.

Therefore, triangles EFA, DBF, FDE, and CED are all congruent.

So, it takes four congruent triangles to make up the area of triangle ABC. Since triangle FDE is one of the congruent triangles that makes up the area of triangle ABC, the ratio of areas of triangle ABD to triangle FDE is exactly 4.

• Click here to explore areas.

Proof (outline): I could not come up with a proof so I'll explain the reasoning I came up with. We know that as P gets closer to any side of triangle ABC the area of triangle DEF decreases causing the ratio of the areas to increase. So, the minimum area ratio would be when triangle DEF is at its maximum area. When P is the centroid, triangle DEF is at its maximum area. In conjecture 2 I proved that the ratio of the areas of the triangles of triangle ABC to triangle DEF is 4 when P is at the centroid. So, as P moves closer to the sides and away from the centroid point, the ratio of the areas will increase. Therefore, the ratio of the areas of triangle ABC to triangle DEF is always four or greater.

Return to Home Page