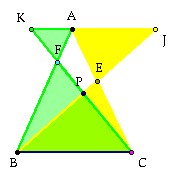
Looking at (BF)(CD)(AE) and (FC)(DA)(EB) for various triangles and various locations of P we discover that
we have some similar triangles. Closer investigation shows that when we take
we get one. Which tells us that the lengths of (BF)(CD)(AE) and (FC)(DA)(EB) have the same distance when multiplied together.
Let us try and prove this. We must draw some parallel lines and form similar triangles.
Triangles BFA' and CFA are similar
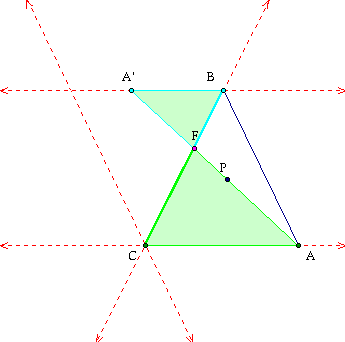
This shows us that BF is proportional to FC these are the first to segments in our equation above.
In addition Triangle BEC is similar to AEC'
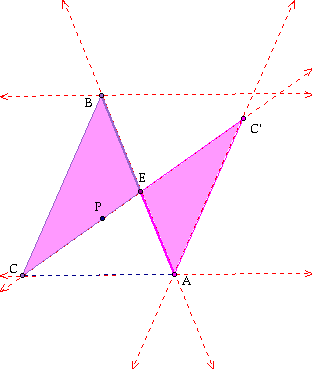
This shows that AE is proportional to EB and these are the last to segments in our equation above.
This should give us an idea that the equation will work out, however here is the final set. Triangle BDA and B'DC are similar
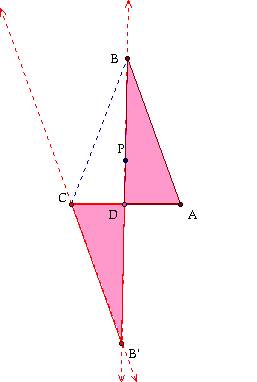
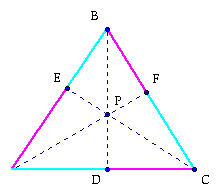
Now we have three triangles that are proportional to themselves and we know what to make them to each other. First let us show what we have currently:
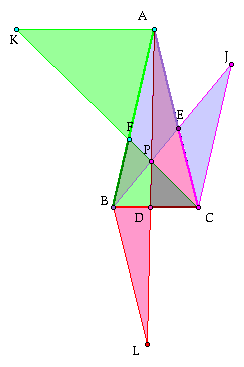
Ok so now that we have some relationships, let us look at how P fits into the situation.
Look at these similar triangles and see if it all connects for yeah?
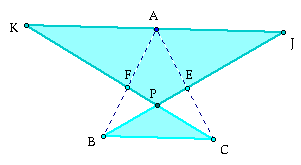
If not how about after we form these similar triangles: