

Three cevians AF, BD, and CE of triangle ABC are concurrent if and only if
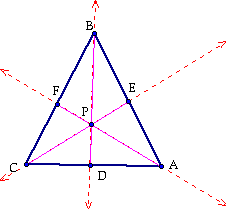
Proof that, if the three cevians are concurrent, then
Through A and C, draw lines parallel to BD. Let the points in which they intersect CE and AF be called K and J.
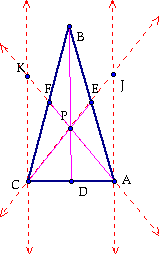
Because of equal vertical angles and equal alternate interior angles Triangle BFP is similar to Triangle CFP and Triangle AEJ is similar to Triangle BEP. Therefore,
Because of the common angle and equal corresponding angles, Triangle CDP is similar to Triangle CAJ and Triangle CAK is similar to Triangle DAP. Therefore,
We can now build the conclusion of Ceva's theorem by multiplying the left and right sides of these equations.
Simplifying we get: