Assignment 4

We consider the triangle below.

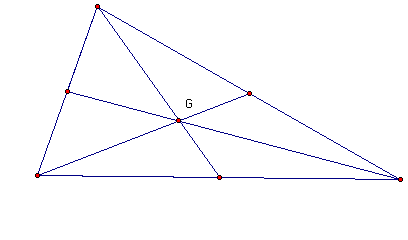
If we draw a segment from each vertex to the opposite side's midpoint, we find that in the above

case, a common point of intersection occurs in the center of the triangle. This is defined as the

Centroid, G. You'll notice that all three segments are concurrent to the Centroid and G appears to be

the center of the triangle....

Things to try with the a triangle and a given centroid

(solutions below)

Question 1 Is it always the case that these lines from each vertex to the midpoint to the opposite

sides are concurrent to G ?

Question 2 Would a triangle's moment or center of mass (if uniformly massive & dense) be the

location of the Centroid?

Question 3 If we can draw a circle inside a triangle that is tangent to all three sides, what is the relaionship

between the radius of the triangle and the centroid?

(hint: construct the circle then explore the triangles that can exist with it have each side tangent to the circle)

To try the above problems out and any others using Geometry Sketchpad 4.0 with the tool below

Solutions to above questions

1. yes

2. yes

3. Answers vary

Proofs and other implications are left to the reader and are classic explorations for high school students.