Centers of a Triangle

By Donna Greenwood

If you're interested in viewing constructions of triangle centers, see write up #5. In this assignment, I'm proving a rather interesting phenomenon about the orthocenter, the circumcenter and the centroid of a given triangle, which is: the three points are collinear. The line defined by these points is called the Euler line. The centroid lies along the segment defined by the circumcenter and orthocenter, 1/3 of the way from the circumcenter to the orthocenter.

In mathematical terms, let H be the orthocenter, C be the circumcenter and G be the centroid. Prove that for any triangle, H, G, and C are collinear, and prove that HC = 2GC.

If you want to manipulate this drawing to see for yourself, click here.

There's also an animated version. These are GSP version 4, so they don't run on earlier versions. The GSP sketch also has some measurements that illustrate HC = 2GC.

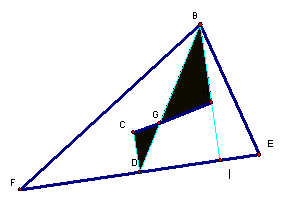
Let BEF be a given triangle. Let H represent the orthocenter, G represent the centroid and C represent the circumcenter.

First of all, add some construction lines to aid in the proof. BI is the altitude from vertex B to side EF, BD is the median from B, and let CD be the perpendicular to EF from C. D is the midpoint of EF. It's worth noting here that CD and BI are parallel lines, since both were constructed as perpendiculars to EF. If we can prove that triangles GCD and GHB are similar with a similarity ratio of 1:2, we're home free!

Any two points determine a line, so let CH determine a line and prove that G lies on that line. CH is a transversal of parallel lines defined by CD and BI. As such, angles DCG and GHB are congruent as alternate interior angles of transversal CH. BD is also a transversal of the parallel lines defined by CD and BI. That gives angle HBG congruent to angle CDG.

By Triangle Angle Sum, we know that the sum of angles in every triangle is 180 degrees, so angle CGD must be equal to angle HGB. If you want to see the arithmetic, click here. Since the two angles at G are equal, we have vertical angles at G, so G must lie on HC. We also have similar triangles GCD and GHB.

To figure out the similarity ratio, remember that G is the centroid of the triangle, and lies on the median BD 1/3 of the way from D to B. That gives DG:GB = 1:2, which is the similarity ratio for triangles GCD and GHB. As corresponding parts of similar triangles, CG:GH = 1:2, or HG = 2GC. QED.

Arithmetic for Triangle Angle Sum

The sum of angles for any triangle is 180 degrees, so the measures of angles GDC + CDG + DCG = 180 and GHB + HBG + HGB = 180. Setting the two equal gives CDG + CGD + DCG = GHB + HBG + HGB. We've proved that the measure of DCG = GHB, and HBG = CDG (since that's what it means for angles to be congruent.) Subtracting those angles from each side leaves CGD = HGB.