An exponential function is of the form:
where b is the base and a positive real number other than 1 and x is any real number.
In this section, we will look at the domain and range of these exponential functions, as well as, look at one specific exponential function, compound interest.
The domain of a function are the possible x-values while the range are the possible y-values. We will find the domain and range by looking at the graphs of some exponential functions.
Example I:
In order to graph the function, f(x) was replaced with y. Now, based on the graph we want to find the domain and range.
Since x is an exponent and the exponent can be any real number the domain is all real numbers which is written as:
D = {all real numbers} From the graph, it looks as if x stops at -5, this is due to the fact the as x decreases, the graph gets closer and closer to the x-axis, but never intersects it and goes below the x-axis. So, this makes the graph look like it stops at -5 when in reality it has just gotten so close to the x-axis that the computer is unable to differentiate between the two.
Now, we need to find the range. The range are the y-values. Since the graph never intersects or goes below the x-axis, the y-values are not zero or negative. This makes the range, all positive real numbers. This is written as:
R = { all positive real numbers} This graph moves upward from left to right and is called exponential growth.
Example II:

Here, having a decimal less than 1 verses a whole number greater than one does not change the domain and range. This means that,
The only difference is that the this graph goes downward from left to right where as the first graph went upward from left to right. This downward slant is known as exponential decay.
What happens if the exponent is negative?
Example III:

Again, the domain and range did not change. All this did was change the direction of the graph. The original graph which is in Example I went upward from left to right where as adding the negative to the exponent made the graph go downward from left to right.
What about if the exponential function is multiplied by a cosntant?
Example IV:
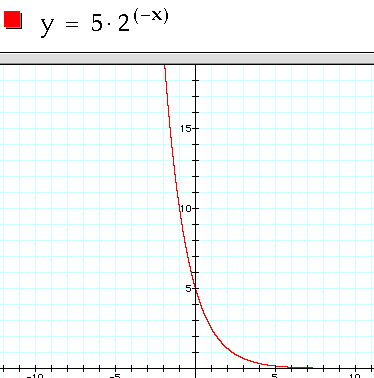
It appears to be very similar to the original. Do you see the difference? Have you figured out what that constant does? If not, play the following movie and see if it helps you to figure out what the constant does to the graph. The original graph will be in purple and the graph in red shows what happens as the value in front of the exponential function changes.
Did that help? Have you figured it out? If so, write a brief one page explanation worth 10 bonus points.
The last idea that we will look at is that of compound interest. That is the total amount of an investment, A, earning compound interest is
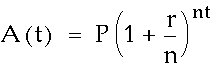
where P is the pricipal, r is the annual interest rate, n is t he number of times interest is compounded per year, and t is the time in years. These problems will be worked as a straight substitution and are thus very simple to solve.