
Proof of Tangent
Circle Construction
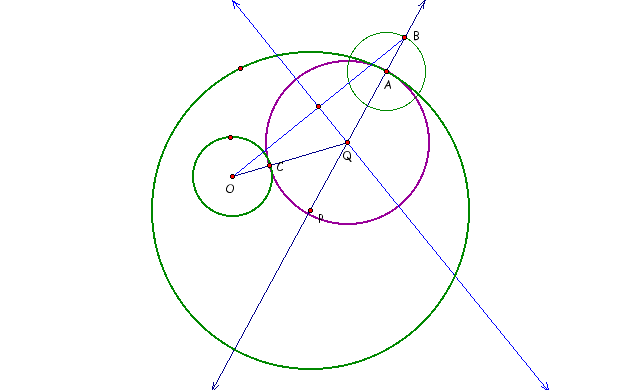
Given: Circles P, A, and O, Isoceles Triangle QOB
Oval Q tangent to Circles O at C and P at A
Circle A equal to Circle O
Proof: Oval Q is in fact a circle.
Need to show that QC = QA
QO = QB by definition of Isoceles Triangle
QO = QC + CO and QB = QA + AB by segment addition
by substitution we know QC + CO = QA + AB
CO = AB since circle O = circle A therefore their respective
radius must be equal.
by substitution QC + AB = QA + AB
by subtraction QC = QA.


