

We can use spreadsheets to help us analyze data and look for mathematical relationships to help us make predictions. For example, take a look at the information we have from th lumber industry that tracks the amount of board feet of lumber that typically is produced from trees in a forest of a certain age:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Let's be sure we agree on how to interpret the table. Based on previous experience, people in the lumber industry claim that, in general, a tree that is 20 years old will provide 100 (1 x 100) board feet of lumber; a 200 year old tree will yield 32,000 (320 x 100) board feet.
A graph of the data might look something like this:
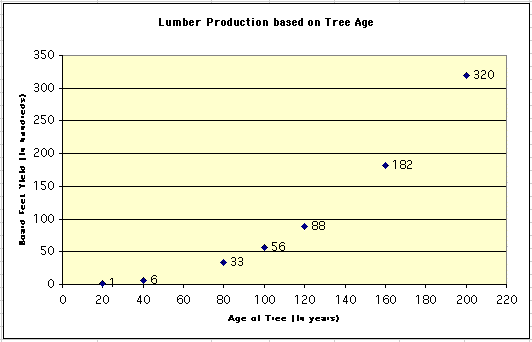
Notice that we do not have data for certain ages. One question that might naturally arise, is how many board feet could a lumber company expect to produce from a 60 year old tree, a 140 year old tree, or a 180 year old tree.
How might you estimate the number of board feet that could be produced for each of those ages?
One possibility is the take the average of the board feet yield for the ages immediately before and immediately after the unknown yield in our data set. For example, to estimate the board feet yield for a 60 year old tree might be to average the yield for a 40 year old and 80 year old trees:
Our estimated board feet yield for a 60 year old tree would be 19.5 (hundred) board feet.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
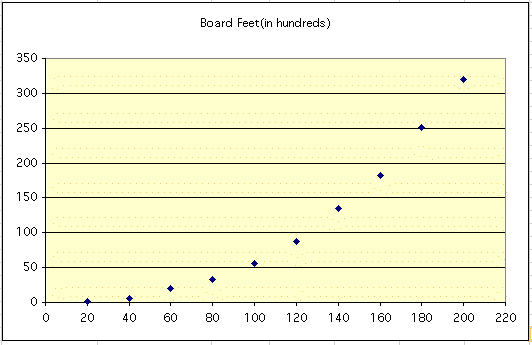
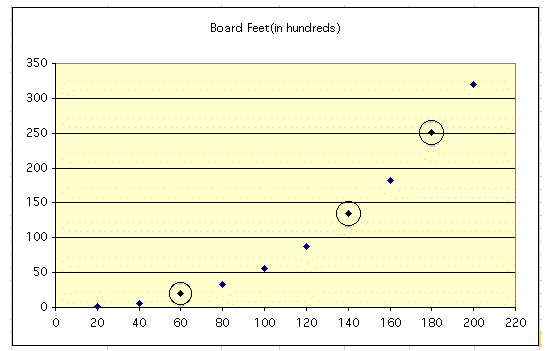
How might we determine how "good" or useful our estimates are? Visually, the estimates seem to "fit" fairly well.
How might we estimate yields for tree that are older than 220
years?
How might we estimate yields for tree that are between the data
years we have? For example, what might be a good estimate yield
for a tree 75 years old?
Something we might want to consider, is the overall behavior of the data. How does the limber yield change as the trees get older?
Try experimenting with the Coefficient: Will you need to increase or decrease the Coefficient to get an estimate close to the original data?
Try experimenting with the Exponent: Will you need to increase or decrease the Exponent to get an estimate close to the original data?
Now try adjusting both the Coefficient and the Exponent: How does an adjustment of the Coefficient affect an adjustment of the Exponent?