Problem: Two Squares (click here to see the problem statement)
My Solutions:

GRAPHIC SOLUTION.

We can see that when AP is relatively small, the combined area of the squares formed by AP and PB is slightly less than the area of the square formed by AB:

 

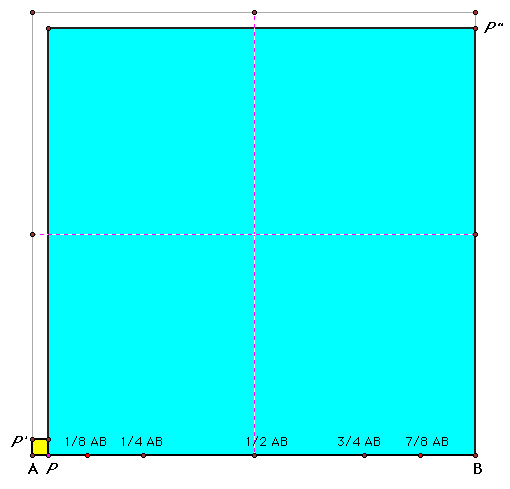
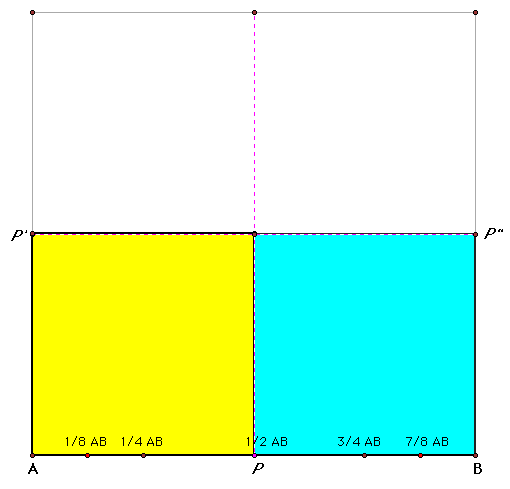
The combined area decreases as we increase the length AP:

 

 

 

 

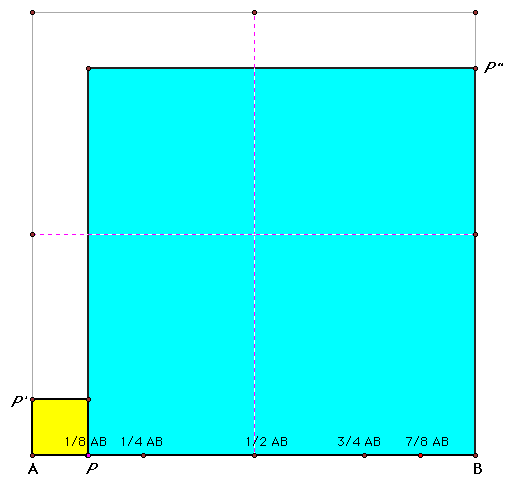
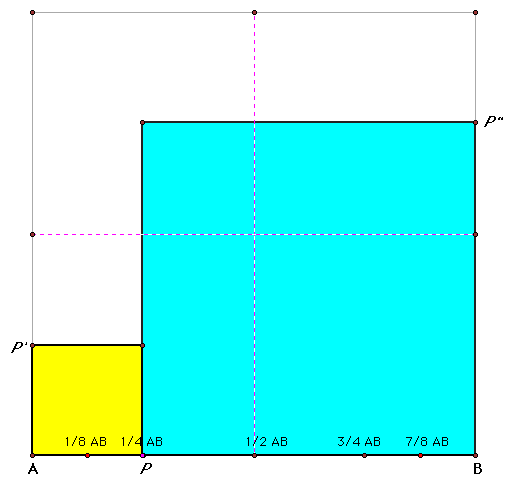
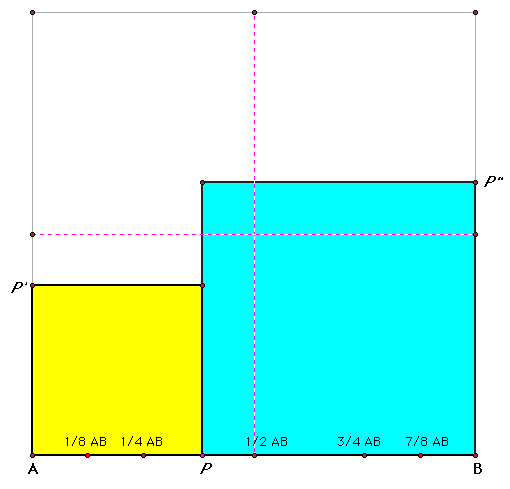
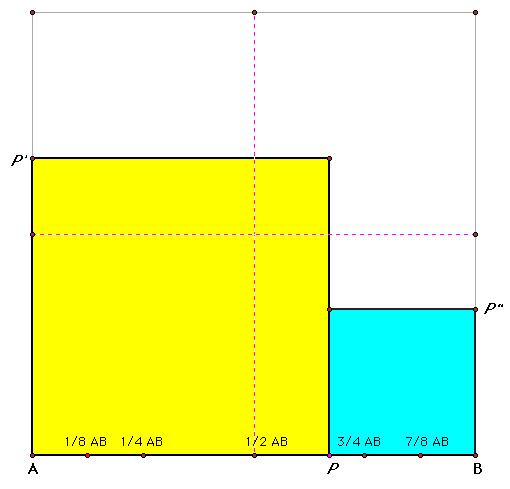
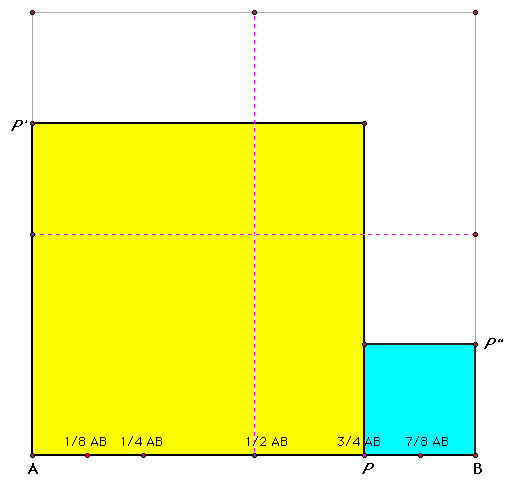
When P is at the midpoint of AB, the combined areas formed by the squares AP and PB equal one-half the area of the square formed by AB.

 

 

 

As AP is increased beyond 1/2 the length of AB, the combined area will now increase, approaching the area of the square formed by AB:

 

 

 

 

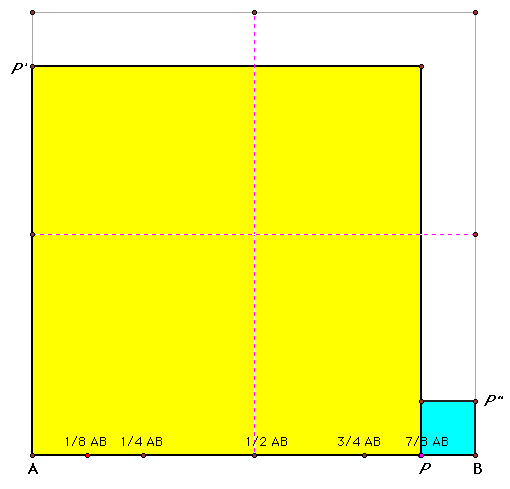
The MAXIMUM combined area is when P is at either A or B: In these cases, one the othe "squares" has an area of zero and the other is equal to the area of the square formed by AB.

Point P should be located at the midpoint of AB to MINIMIZE the combined areas of the squares formed by AP and PB.

For an ANIMATED VERSION of the graphic representation,
Open Geometer's Sketchpad then Click Here

ALGEBRAIC SOLUTION.

Let's look at AP in increments of 1/8. When AP = 1/8AB, then PB = 7/8AB. The combined areas of the squares formed by each segment will then be

 

When AP = 2/8AB, then PB = 6/8AB, so the combined area will be

 

When AP = 3/8AB, then PB = 5/8AB, so the combined area will be

 

When AP = 4/8AB, then PB = 4/8AB, so the combined area will be

 

When AP = 5/8AB, then PB = 3/8AB, and the combined area will be the same as AP = 3/8AB and PB = 5/8AB. Again, the minimum combined area is 1/2 of the area of the square formed by AB.