NAME:___________________ DATE:___________________
For problems 1 and 2, plot the points, graph
the line that contains these two points, and find the slope of
the line. USE YOUR GRAPH PAPER!
1) (0,3); (3,6)
2) (5,4); (1,6)
3) Verify if the following ordered pairs are
solutions for the following equation: 3x 2y = 12
a. (1,7)
b. (0,-6)
c. (-1,3)
4) Graph the equation 2x + y = 3 using a table of values. Remember, you must have 5 ordered pairs. USE YOUR GRAPH PAPER WHEN GRAPHING!
For problems 5 and 6, find the x and y intercepts
of the equation and use them to graph the equation. USE YOUR GRAPH
PAPER!
5) 9x + 3y = 9
6) y 4x = 2
7) You are starting a business and are going to sell calculators. You start off with 100 calculators and know that after 20 days, all of your calculators will be sold. The equation of the line that models this selling of calculators is y = -5x + 100, where 5, the slope, is how many calculators you sell per day, and 100 is the number of calculators that you start with. You know that you will need to reorder more calculators 5 days before you run out so that the new ones will have time to get to your store. Graph the equation above and tell how many calculators you will have when you reorder. Use your knowledge of x and y intercepts to figure this out. USE YOUR GRAPH PAPER WHEN GRAPHING THE LINE!
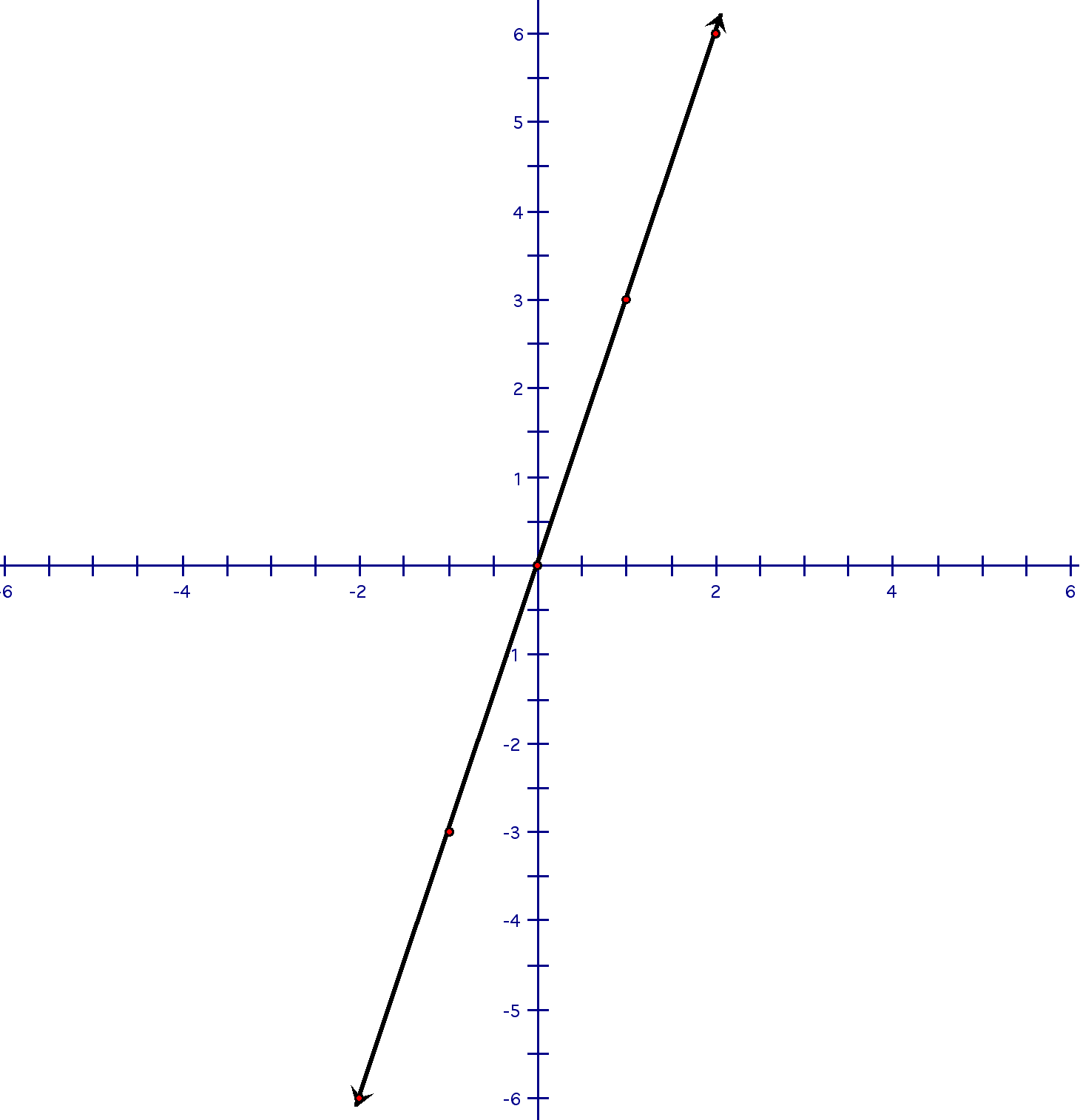
For problems 8 and 9, find the slope of the given line.
8)

9)
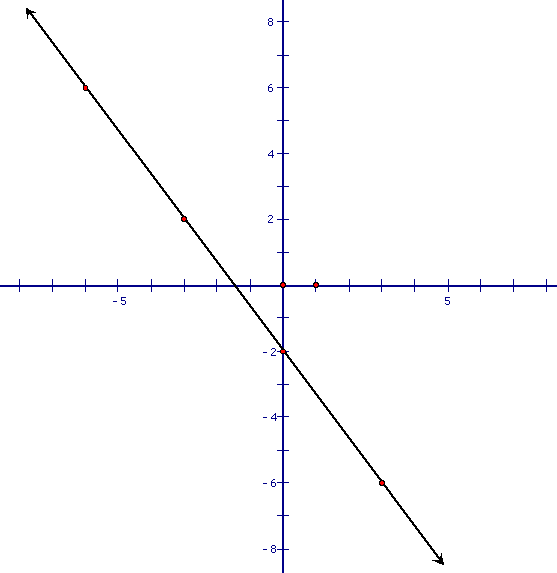
10) Find the constant of variation, k, when x = 3 and y = -8, and write the direct variation equation.
11) Write the equation, 7x + 3y = 12 in slope-intercept form and identify the slope and the y intercept.
For problems 12 and 13, graph the following
equations using the slope intercept form of the line. USE YOUR
GRAPH PAPER!
12) y = 2x 6
13) 2y 4x = 10
14) Suppose you and a friend are going on a hike in the Painted Desert in the western U.S. You are on vacation in the middle of the summer and it is deadly hot outside. You and your friend are going to start your hike at 10:00 a.m. You know that when you start, the temperature will be 92 degrees. The temperature will rise 2 degrees every hour and you can stand to be out hiking until it reaches 106 degrees. When it gets that hot, you need to be back from hiking. The equation that models this data is y = 2x + 92, where 2, the slope, is how much the temperature rises every hour, and 92 is the temperature at the start of your hike. First, graph the equation above. Then answer the following questions. How many hours can you be out hiking? What time do you need to turn around and come back? What is the temperature after 5 hours? USE YOUR GRAPH PAPER WHEN GRAPHING THE LINE!
15) Which pairs of lines are parallel?
a) y = 3x + 2; y = -x + 2
b) 4x 4y = 12; y = x + 2
c) -4y = 12x 3; 3y = -9x 2
d) 2y + 12x = 3; y = 6x 10
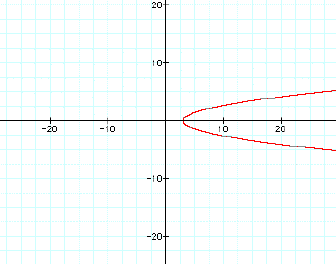
For problems 16 and 17, identify whether or
not the relations are functions.
16)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17)
18) Evaluate the function f(x) = 2x 1
for the following values of x:
a) x = 3
b) x = 0
c) x = -2
For problems 19 and 20, graph the linear function.
USE YOUR GRAPH PAPER!
19) f(x) = -2x + 5
20) f(x) = 4x - 3