

In order to the observation, we notice the graph is always
the central symmetry with the center point of the origin. We can
observe or proof this feature according to search the intersections
of ![]() and
and ![]() . By this observation, we also
notice these equations haven't three intersections always. Through
algebraic approach of the equation, proof the feature of the central
symmetry and search the intersections of the equations.
. By this observation, we also
notice these equations haven't three intersections always. Through
algebraic approach of the equation, proof the feature of the central
symmetry and search the intersections of the equations.
Substance ![]() for
for![]()
Then
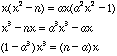
When ![]() the equation is conclusion with
the equation is conclusion with ![]() .Therefore,
if
.Therefore,
if ![]() is any number, there is the intersection of the
origin.
is any number, there is the intersection of the
origin.
When ![]() then
then
![]()
When ![]()
![]() because its discriminant is
because its discriminant is ![]()
so ![]()
Substance ![]() for
for ![]() then
then ![]()
Therefore, when ![]() and
and![]() , intersections
of the equations accord with
, intersections
of the equations accord with![]() .
.
When ![]() and
and![]() ,it
is not true, then there is only intersection of the origin.
,it
is not true, then there is only intersection of the origin.
When ![]() that is to say
that is to say ![]()
Then
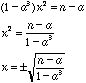
and
![]()
So, when ![]() , the coordinates of the intersection of the equations
without the origin are below.
, the coordinates of the intersection of the equations
without the origin are below.
![]()
Only the signs differ from coordinates of two intersections , so these two points are the central symmetry with the central point of the origin.
For these coordinate numbers are the real numbers :
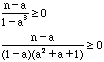
So ![]() and
and ![]()
Or ![]() and
and ![]()
Because of ![]() and
and ![]()
For ![]() and
and ![]() ,when
,when ![]() then
then
![]() ,when
,when ![]() then
then ![]()
For ![]() and
and ![]() ,when
,when ![]() then
then
![]() ,when
,when ![]() then
then ![]()
Therefore, when ![]() ,
, ![]() or
or
![]()
and when ![]() ,
, ![]() or
or ![]()
As ![]() , then
, then ![]()
So when ![]() , the intersection is the only (0,0)
, the intersection is the only (0,0)
Conclusion
As ![]() and
and ![]() or
or ![]() ,or
as
,or
as ![]() and
and ![]() or
or ![]() , then
there are three intersections of
, then
there are three intersections of
![]() .
.
The first two points differ from only signs . It means central symmetry with center point of the origin.
As ![]() and
and ![]() , or as
, or as ![]() and
and
![]() , then there is an only intersection of the origin.
, then there is an only intersection of the origin.