Clay Bennett

Assignment 11.1

In this investigation, I will be exploring polar equations. Polar equations is another subject that I have not had much experience with. We dabbled with polar equations a little in my high school calculus class, but other than that I have not really worked with polar equations. The focus of my investigation will be on the equations…

I will begin by examining the first equation. Here is a picture of its graph when all of the variables are equal to one.

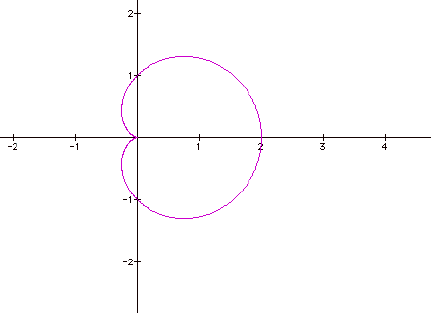
In high school, we referred to this plot as the butt-print (teacher included), but from this I assignment I have learned that it has a formal name, the n-leaf rose. My next step in this investigation was to began playing around for the values of a. My conclusion was that when an absolute value got larger and b and k stay at one its graph became a circle with a radius equal to a and a center point of one. Here is a picture of the equation when a = 10 and when a = -10 while b and k =1.

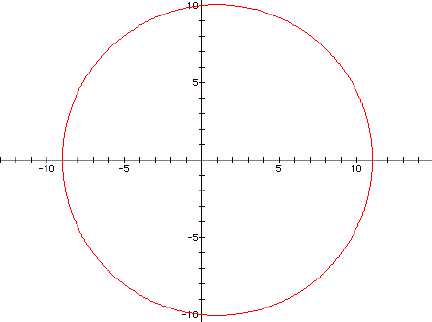
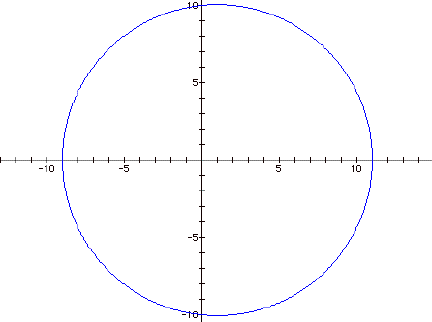
As you can see, it doesn't matter if the value of a is negative or positive. Next, I began to explore a when it was very close to zero. This did not prove to be interesting because it just gave the graph of

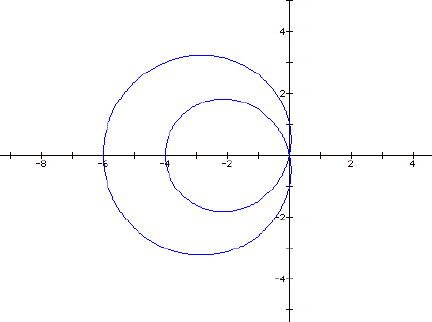
Next, I began to look at the values of b when a and k =1. When b became larger, the loop within the circle became larger.

Graph for when b=5.

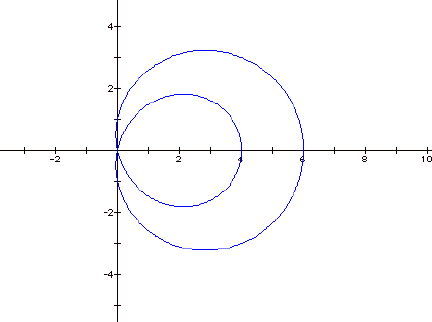
As it got extremely large, the inside loop would almost be the same as the outside loop. I would imagine if you took the limit of b -> infinity then the two loops would be equal. Graph for when b = 1000.

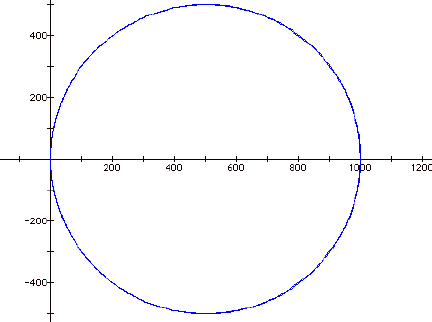
When I took b to be less than zero the same thing happened, the only exception was that the graph was reflected across the y-axis.

Graph of b = -5.

Graph of b = -1000.

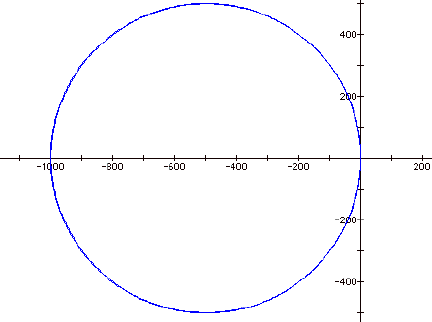
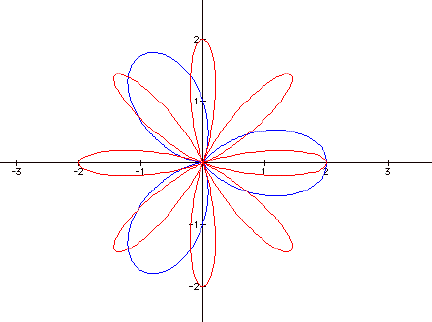
Next, I looked at b when it approached zero. I discovered that as b approaches zero then the graph becomes the unit circle or r = 1, which makes sense. Finally, I underwent the same investigations with the k value. I found k to be very interesting. I've probably said that I've found something interesting a lot throughout these assignments, but I really mean it this time. For every value of k there would be abs(k) number of loops. This really impressed me. Here is a picture for when k= 3 and 8.

When k got really big, then the outline of the n-leaf rose began to appear. Here is a picture.

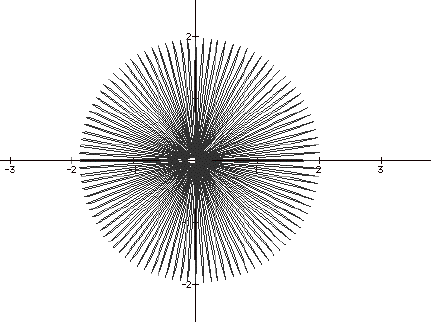
Lastly, I looked at k when it approached zero, which would give us r = 1 + 1 => a circle with center (0, 0) and radius equal to 2.

I really feel I got something out of this investigation. I have definitely spent the most time on this one out of all the others. I will definitely continue to play with this equation.