
Clay Bennett
Assignment
1.6
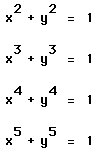
In
this assignment, I am required to graph a series of equations and make predictions
as to what a later series of equations will look like when graphed. The equations I am supposed to graph
are as follows:
![]()
I will start by graphing and commenting on them
individually. The first graph,
,
will obviously be a circle.
No real surprise there.
![]()
I am not sure what the rest of the graphs will
look like. I would not think that
the equations would be circles.
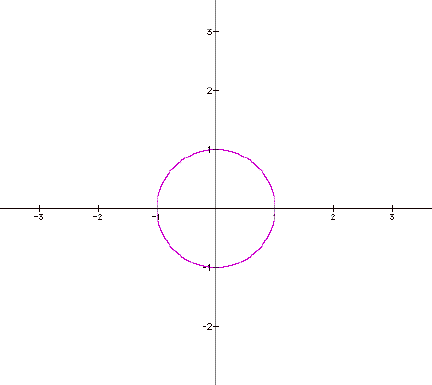
Now I will graph
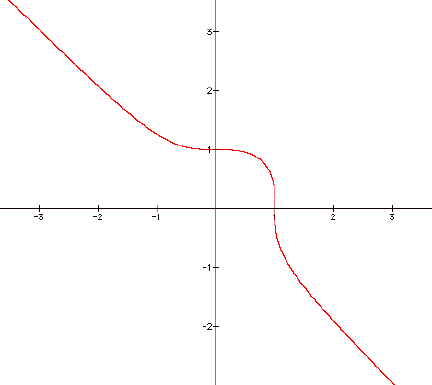
I did not expect this to be the out come. I was expecting a closed figure with a
shape other than a circle.
![]()
Now I will move on to graphing
I
really did not have an idea of what to expect from this equation, but this
graph does not really surprise me.
![]()
Next, I will graph
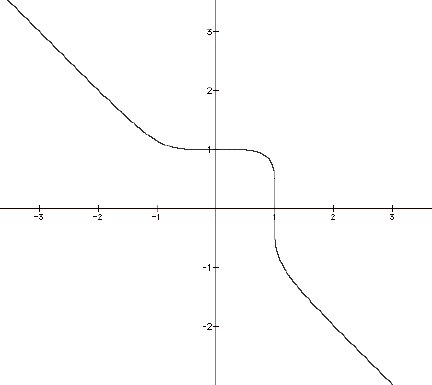
In this graph, it seems to show that as the odd
exponents get larger; its asymptotes approach the -(x)=y line. I will show more on this a little
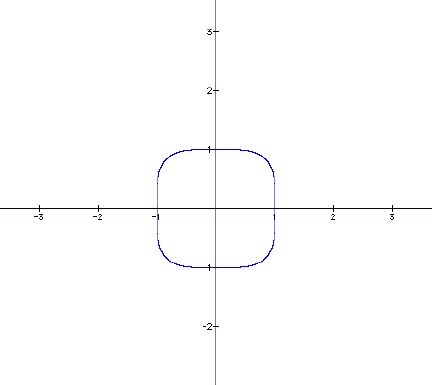
later. Now I will graph the final
equation,
![]()
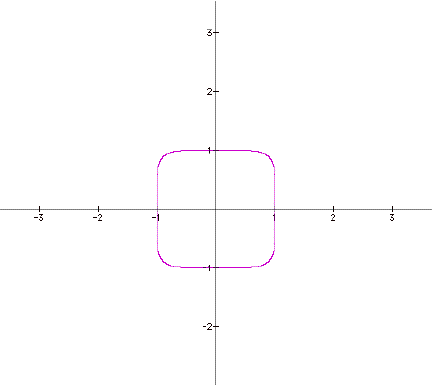
This graph seems to show that the higher the
even exponents get the more square-shaped the graph becomes. Now I am going to graph all of the
equations together so I can see more trends. I am also going to graph the
-(x)
= y line.
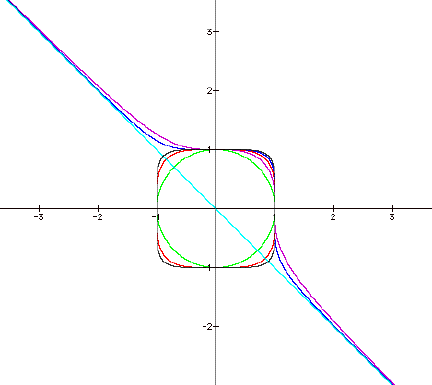
After graphing all of the equations on the same
plane it is much easier to see trends.
As you can see the -(x) = y line is a line of symmetry for the equations
with even exponents. As I stated
earlier, the equations with odd exponents has asymptotes that approach the -(x)
= y line. They seem to converge on
it sooner as the odd exponents get larger. The odd equations also seem to be getting closer to the to
forming the top half the equations with even exponents. The equations with the even exponents
start with a circle and as the exponents get larger they seem to form a 1 x 1
square. Each time the exponent
increases, its corner gets closer to the point (1,1). My prediction for the equations for when the exponents are
24 and 25 are that they even exponent will be almost a perfect square and the
odd exponent will be very close to being the top half of the even exponent and
will almost converge at the -(x) = y line at points (-1,1) and (1,-1). Now lets graph
![]()
![]()
![]()
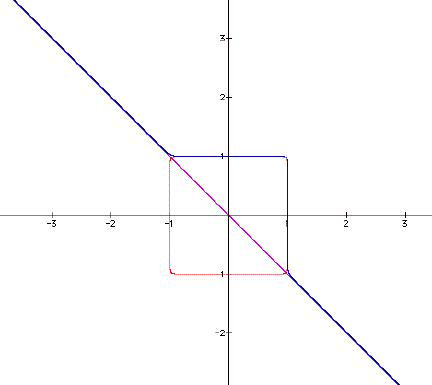
As you can see my predictions were correct. When I began this investigation I did
not expect this to be the outcome.
One other thing I stumbled across due to a typing error on my part was
what happens when one exponent is odd and the other is even. Here is a graph of it for no extra
charge.
![]()
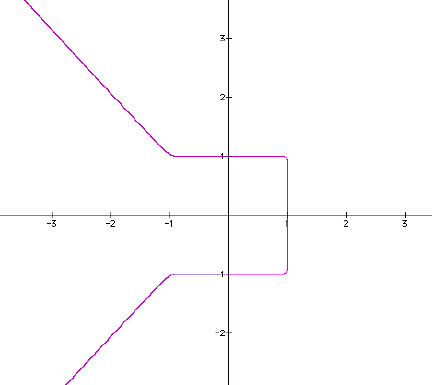
![]()
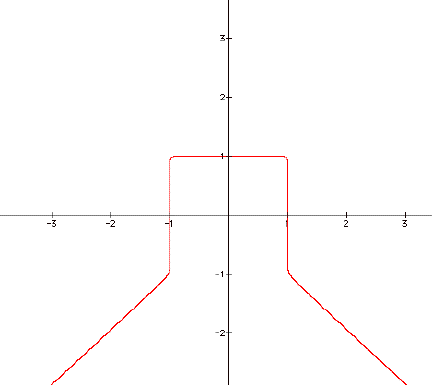
I
changed my mind. If you looked at
those last two graphs then it will be $5.00. Cash only. You
are on the honor system.